組合せとグラフの理論（塩田）2024年度

組合せとグラフの理論（塩田）第1回 (2)　グラフ理論の始まり

ケーニヒスベルクの７つの橋渡り

　グラフ理論で扱う「グラフ」とはどんなものか、を理解してもらうために、グラフ理論が生まれたエピソードを紹介します。

　18世紀初め、ロシア、ケーニヒスベルクの町で「７つの橋渡り」という遊びが流行りました。プルーゲル川の両岸と２つの中洲に架かる７つの橋を丁度１回ずつ渡って出発点に帰って来れるか、というクイズです。

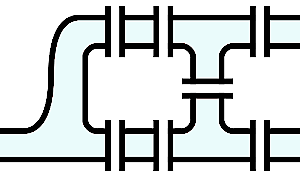
ちょっと試してみてください。うまくいかないはずです。

オイラー先生に HELP!

　もし不可能なら不可能であることを証明してもらいたい、ということでオイラー先生に HELP が掛かりました。

　オイラー先生は1707年生まれの大数学者。1771年頃に失明するもなお1783年に76歳で没するまで研究を続け、書いた論文は合計5万ページを超えます。

　オイラー先生は

岸や中洲を頂点
橋を辺

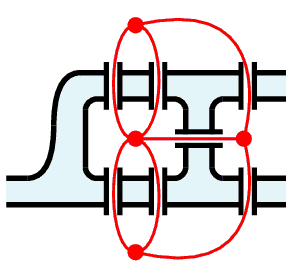
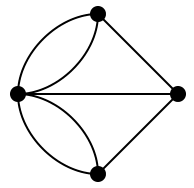
として地図を抽象化することを思い付きました。（面である岸や中洲を点にしてしまうというこの大胆な発想 !! ）頂点は、それらが表す岸や中洲が橋でつながっているときに、辺で結ぶことにします。するとこんな絵が得られます：

赤い部分を抜き出すとこんな図形です：

※　このようにモノのつながりを表現した図形（と言うか構造）を「グラフ」と呼びます。

一筆書きの定理

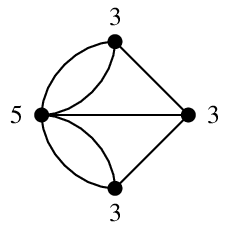
　さて、橋渡りのクイズは、このグラフで出発点に戻る一筆書きができるか、という問題に言い換えることができます。そしてオイラー先生は「一筆書きの定理」を証明することによって、橋渡りが不可能であることを証明しました：

定理　連結なグラフでは、出発点に戻る一筆書きができることと、全ての頂点の次数が偶数であることが同値である。（ひとつの頂点に接続している辺の本数を専門用語で次数と言います。）

橋渡りのグラフでは４つの頂点の次数が 5, 3, 3, 3 ですので一筆書きができないことがわかります。

※　オイラー先生が1736年に示したのは、出発点に戻る一筆書きができるなら次数は全て偶数、の方で、次数が全て偶数なら出発点に戻る一筆書きができる、の方は100年以上のちにヒールホルツァーが示しました。

前へ / 戻る / 次へ