組合せとグラフの理論（塩田）2023年度

組合せとグラフの理論（塩田）第6回 (5)　幅優先探索・深さ優先探索の応用

　幅優先探索・深さ優先探索を応用したいろんなグラフアルゴリズムを紹介します。

幅優先探索の応用：最短路

Th.20　幅優先探索木は、根から他の頂点への最短路を与える。

Ex.21 　次のグラフ

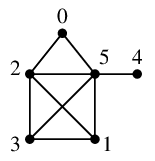
の、$0$ を根とする幅優先探索木は

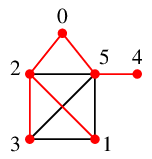
です。これは根 $0$ から $2$, $5$ へは最短距離 $1$, 根 $0$ から $1$, $3$, $4$ へは最短距離 $2$ であることを表しています。

※　辺の長さは１、と考えての話です。辺ごとに「長さ」を設定しているグラフの最短路問題は後日やります。

深さ優先探索の応用：カット点判定

Def.22　深さ優先探索木においては親子関係が考えられ、根に近い方の頂点を祖先、根から遠い方の頂点を子孫と定める。

Ex.23 　Ex.21 のグラフの $\require{cancel}\cancel{0}$ $\require{color}\textcolor{red}{2}$ を根とする深さ優先探索木は ... 6月1日訂正

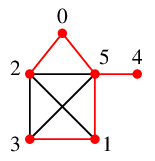$\longrightarrow$

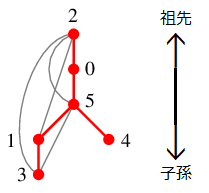
となります。根 $2$ の子は $0$、$0$ の子は $5$、$5$ の子は $1$ と $4$、$1$ の子は $3$ と考えます。

Th.24　深さ優先探索木に使われなかった辺は、必ず祖先と子孫をつなぐ。

証明　子孫同士が結ばれていれば祖先にバックトラックしていないはずなので。(証明終)

Th.25　連結グラフ $G$ の頂点 $v$ を根とする深さ優先探索木を $T$ とするとき、 $v$ が $G$ のカット点であること $\Leftrightarrow$ $T$ において $v$ の子が 2 人以上いること

証明　Th.24 より、$T-v$ に使われていない $G-v$ の辺は $T-v$ の同一連結成分の頂点同士しか結びません。従って $T-v$ の連結成分の個数は $G-v$ の連結成分の個数に一致します。

	$\longrightarrow$
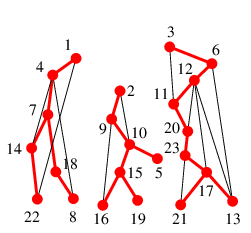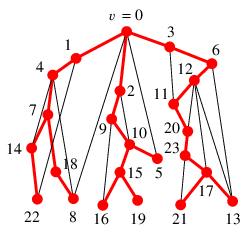
$G$ と $\require{color}\textcolor{red}{T}$		$G-v$ と $\textcolor{red}{T-v}$

　$T$ において $v$ の子がひとりしかいときは $v$ は $T$ の端点であり $T-v$ は連結、従って $G-v$ も連結です。 $T$ において $v$ の子がふたり以上いるときは $T-v$ は非連結になり、従って $G-v$ も非連結です。 (証明終)

他にも

　非連結なグラフでも幅優先探索・深さ優先探索を行うことができて、こんな応用もあります：

道の探索

道の探索
$u$ を根とする探索で $v$ が探索できれば探索木の中に $u-v$ 道があり、そうでなければ $u-v$ 道は存在しません。
橋の判定

橋の判定
$e=uv$ を除去したグラフ $G-e$ で $u$ を根とする探索を実行し、 $v$ が探索できれば $e$ は橋でなく、そうでなければ $e$ は橋です。( L'a 6 )
連結成分への分解

連結成分への分解
$u$ を根とする探索木に属する頂点たちと、それらを結ぶ辺たちが作る部分グラフが、$u$ の属する連結成分です。未探索点から探索を始めれば次の連結成分がわかります。

この３つのアルゴリズムでは探索は幅優先でも深さ優先でも構いませんが、道の探索では幅優先の方が最短路が見つかって嬉しいです。