組合せとグラフの理論（塩田）第6回 (4)　深さ優先探索
前へ / 戻る / 次へ

深さ優先探索のアルゴリズム

　次は 深さ を優先して探索します。
Algorithm 15（深さ優先探索、DFS = Depth First Search ）
  • 入力：連結なグラフ $G$ と、その頂点 $v$
  • 出力：$v$ を根とする $G$ の深さ優先探索木 $T$
  1. $T$ の初期値は $v$ １点からなる木とし、最初の現在地を $x = v$ とする。
  2. $x$ の未探索隣接点があれば、そのうち番号の一番小さいものを $y$ とする。 そうでなければ 4° へ。
  3. $T$ に辺 $xy$ を付加し、次の現在地を (新$x$) $=y$ として 2°へ戻る。 ( $x$ を「$y$ の親」と呼ぶ。)
  4. $x=v$ であれば終了。そうでなければ「$x$ の親」を次の現在地 (新$x$) として、2°へ戻る。
ステップ 4° の操作をバックトラックと呼びます。
Rem.16（ここ大事！）　深さ優先探索の要点は
  • 探索木 $T$ には辺は 1 本ずつしか付加しない
  • 現在地に未探索な隣接点がある限り、深く深く 進んでゆく
  • 現在地に未探索な隣接点が無い時は、$T$ の辺をたどって「親」へ戻る
ことです。

例題

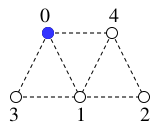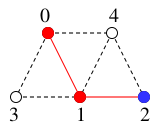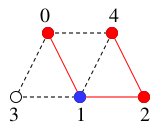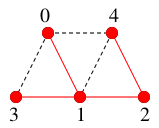
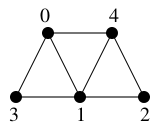
Ex.17　 入力を $G=$ , $v=0$ とします。
( Ex 12 の $G$ とは頂点番号を変えてあるので注意。)
  1. $0$ を探索済みとし、 $T=$ 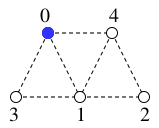, $x=0$ を最初の現在地とします。
    ( 青い頂点 が現在地です。)
  2. 現在地 $x=0$ の未探索な隣接点 $1$, $3$, $4$ のうち番号が一番小さいものは $y=1$ .
  3. $y=1$ を探索済みとし、 $T$ には辺 $01$ を付加して $T=$ ,
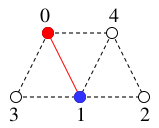    (新$x$)$=1$ .
  4. 現在地 $x=1$ の未探索な隣接点 $2$, $3$, $4$ のうち番号が一番小さいものは $y=2$ .
  5. $y=2$ を探索済みとし、 $T$ には辺 $12$ を付加して $T=$ ,
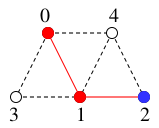    (新$x$)$=2$.
  6. 現在地 $x=2$ の未探索な隣接点は $y=4$.
  7. $y=4$ を探索済みとし、 $T$ には辺 $24$ を付加して $T=$ ,
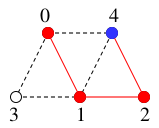    (新$x$)$=4$.
  8. 現在地 $x=4$ には未探索な隣接点は無い.
  9. $4$ の親 $2$ へバックトラックし、 $T=$ 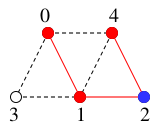, (新$x$)$=2$.
  10. 現在地 $x=2$ にも未探索な隣接点は無い.
  11. $2$ の親 $1$ へバックトラックし、 $T=$ 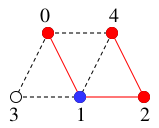, (新$x$)$=1$.
  12. 現在地 $x=1$ の未探索な隣接点は $y=3$.
  13. $y=3$ を探索済みとし、 $T$ には辺 $13$ を付加して $T=$ ,
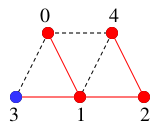    (新$x$)$=3$.
手でやるときは、未探索点が無くなったのでここで終了すればよく、
$T=$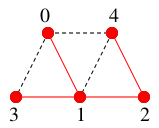
となります。( アルゴリズム的にはこのあと、$1$, $0$ へバックトラックして終了となります。)
手順を表にしてまとめておくと
現在地 $x$$x$ の未探索な隣接点動作探索木 $T$ に付加する辺
$0$$1$, $3$, $4$$1$ へ進む$01$
$1$$2$, $3$, $4$$2$ へ進む$12$
$2$$4$$4$ へ進む$24$
$4$無し$2$ へバックトラック無し
$2$無し$1$ へバックトラック無し
$1$$3$$3$ へ進む$13$

Ex.17' 　入力を同じグラフ $G=$ とし、根を $v=1$ とすると、手順は

現在地 $x$$x$ の未探索な隣接点動作探索木 $T$ に付加する辺
$1$$0$, $2$, $3$, $4$$0$ へ進む$10$
$0$$3$, $4$$3$ へ進む$03$
$3$無し$0$ へバックトラック無し
$0$$4$$4$ へ進む$04$
$4$$2$$2$ へ進む$42$

となり、深さ優先探索木は
$T=$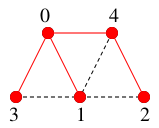
となります。

Ex.17'' 　三たび同じグラフ $G=$ で、根を $v=3$ とした場合、手順は
現在地 $x$$x$ の未探索な隣接点動作探索木 $T$ に付加する辺
$3$$0$, $1$$0$ へ進む$30$
$0$$1$, $4$$1$ へ進む$01$
$1$$2$, $4$$2$ へ進む$12$
$2$$4$$4$ へ進む$24$

となり、深さ優先探索木は
$T=$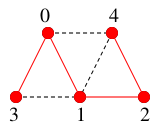
となります。

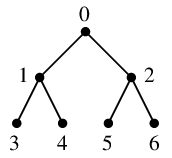
Ex.18 　二分木 $T=$ はそれ自体が全域木ですが、$v=0$ を根とする深さ優先探索の手順は

現在地 $x$$x$ の未探索な隣接点動作探索木に付加する辺
$0$$1$, $2$$1$ へ進む$01$
$1$$3$, $4$$3$ へ進む$13$
$3$無し$1$ へバックトラック無し
$1$$4$$4$ へ進む$14$
$4$無し$1$ へバックトラック無し
$1$無し$0$ へバックトラック無し
$0$$2$$2$ へ進む$02$
$2$$5$, $6$$5$ へ進む$25$
$5$無し$2$ へバックトラック無し
$2$$6$$6$ へ進む$26$

となります。すなわち頂点が探索される順番は $$0,\ 1,\ 3,\ 4,\ 2,\ 5,\ 6$$ となります。

※　こちらも慣れてくればグラフの絵ひとつだけでできるようになります。

深さ優先探索の言い換え

　このアルゴリズムは、スタックを用いて次のように言い換えることができます。
Algorithm 19（深さ優先探索の言い換え ）
  • 入力：連結なグラフ $G$ と、その頂点 $v$
  • 出力：$v$ を根とする $G$ の深さ優先探索木 $T$
  1. 空スタック $S=\{\ \}$ を作り、$T$ の初期値は $v$ １点からなる木とする。
  2. 現在地を $x=v$ とする。
  3. $x$ の未探索な隣接点があれば、そのうち 番号の一番小さいもの を $y$ とする。 そうでなければ 5° へ。
  4. $S$ の先頭に $x$ を追加し、$T$ には辺 $xy$ を付加する。現在地を (新$x$)$=y$ として 3°へ戻る。
  5. $S$ が空(くう)であれば終了。 そうでなければ $S$ の先頭から $x$ を取り出して現在地とし、3°へ戻る。

前へ / 戻る / 次へ