組合せとグラフの理論(塩田)第7回 (4) 閉路部分空間 $W(G)$
閉路部分空間 $W(G)$
これもまず定義から。
Def.10 $G$ 内の閉路たちから $\oplus$ で作り出せる辺の部分集合全ての集合を $W(G)$ と表し、
「$G$ の閉路部分空間」と呼ぶ。$\emptyset$ も $W(G)$ の要素のひとつとする。
Rem.11 閉路それ自身も全て $W(G)$ の要素である。
Th.12 $W(G)$ は $\mathbb{F}_2$ 上のベクトル空間になる:
- 加法は $\oplus$
- ゼロは $\emptyset$
- 2倍はゼロなので、スカラーは $\mathbb{F}_2$
証明 Th.7-9 より。
$W(G)$ がベクトル空間になることがわかりましたので、あとは「基底ベクトル」をみつけさえすれば
$W(G)$ 内の全てのベクトル、特に $G$ の全ての閉路を統制できることになります。
基本閉路集合
Def.13 $G$ を連結グラフ、$T$ をその全域木のひとつとする。
$T$ に属さない $G$ の辺 $e$ を $T$ に付加すると閉路 $C_e$ が 1 つだけできる(第6回 Th.5)。
そのような $C_e$ 全ての集合を ${\cal F}(T)$ と表し、「$T$ に関連した基本閉路集合」と呼ぶ。
Ex.14 Ex.6 と同じグラフ
$G=$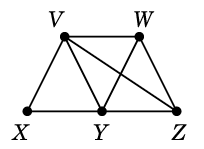
において、全域木
$T=$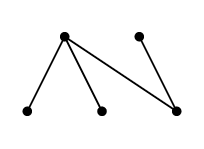
を選んだとしましょう。このとき $T$ に属さない辺は次の $e$, $f$, $g$, $h$ の 4 本です。
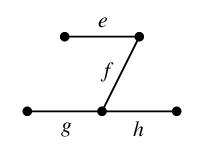
$T$ に $e$ を付加すると、次のように閉路でき(赤い部分)、これが $C_e$ です。
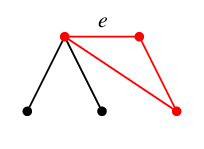
同様に $T$ に $f$ を付加してできる閉路が $C_f$,
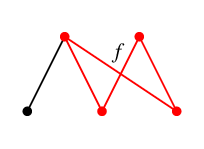
$T$ に $g$ を付加してできる閉路が $C_g$,
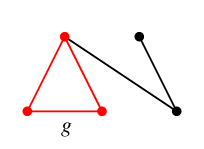
$T$ に $h$ を付加してできる閉路が $C_h$ です。
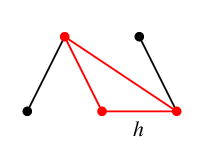
結局、$T$ に関連した基本閉路集合 ${\cal F}(T)$ は
となります。
Th.15 ${\cal F}(T)$ は $W(G)$ の基底になる。すなわち
- 全ての閉路は、基本閉路と $\oplus$ で作ることができる。ここが肝心!!
- $\dim W(G) = m - n + 1$. ( ただし、$G$ の頂点数を $n$, 辺数を $m$ とする。)
証明 (1) 基本閉路 $C_e$, $C_f$, $\cdots$ を係数 1 で足し合わせると、
$C_e \oplus C_f \oplus \cdots = \{\,e,f,\cdots\,\} \neq \emptyset$
であり、これは基本閉路たちが一次独立であることを意味しています。
そして、任意の閉路 $C$ は次のアルゴリズム
Alg.16 によって基本閉路の和として表すことができます。
(2) 次元とは基底ベクトルの個数のことであり、それは $T$ に属さない $G$ の辺の本数でしたから
$\dim W(G) =$ ( $G$ の辺数 ) $-$ ( $T$ の辺数 ) $=m - (n - 1)$.
(証明終)
閉路を基本閉路の和に表すアルゴリズム
Algorithm 16
- 入力:$G$ の閉路 $C$
- 出力:$C$ を基本閉路の和として表す表し方
- $T$ に属さない $C$ の辺を $e$, $f$, $\cdots$, $h$ とする。
- $C_e \oplus C_f \oplus \cdots C_h$ を出力する。
証明 $D=C_e \oplus C_f \oplus \cdots C_h$ とおくと、
$e$, $f$, $\cdots$, $h$ は全て $C$ と $D$ に 1 回ずつ含まれますので、$C \oplus D$ には含まれません。
すなわち $C \oplus D$ は $T$ の辺の部分集合になります。
Th.5 から $C \oplus D$ は 閉路に分けられるはずですが、$T$ は閉路を含みませんので、結局
$C \oplus D=\emptyset$. よって $C = -D = D$.
(証明終)
Ex.17 Ex.14 の状況
$G=$ $T=$
$T=$
では $W(G)$ の次元は $4$ で、
が $W(G)$ の基底です。その要素は
$\emptyset,\quad C_e,\quad C_f,\quad C_g,\quad C_h,$
$C_e \oplus C_f,\quad C_e \oplus C_g,\quad C_e \oplus C_h,\quad C_f \oplus C_g,\quad C_f \oplus C_h,\quad C_g \oplus C_h,$
$C_e \oplus C_f \oplus C_g,\quad C_e \oplus C_f \oplus C_h,\quad C_e \oplus C_g \oplus C_h,\quad C_f \oplus C_g \oplus C_h$
$C_e \oplus C_f \oplus C_g \oplus C_h$
の 16 個となります。
Alg.16 を実行してみましょう。入力を
$C=$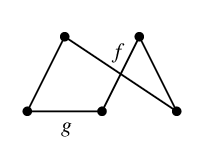
とします。このとき $T$ に属さない $C$ の辺は $f$, $g$ の 2 本です。
$C_f=$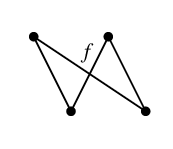 と
$C_g=$
と
$C_g=$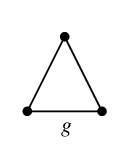
を重ねて描くと
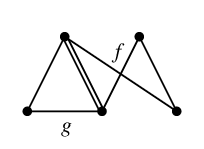
二重辺を消して
$C_f \oplus C_g=$

$C$ になりましたね。
やってみよう Ex.17 の状況で、今度は
$C'=$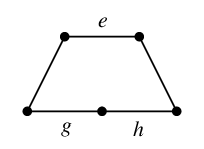
を入力として
Alg.16 を実行してみましょう。
答え
$T$ に属さない $C'$ の辺は $e$, $g$, $h$ の 3 本です。
$C_g=$ $C_h=$
$C_h=$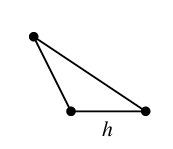 $C_e=$
$C_e=$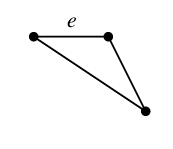
を重ねて描くと
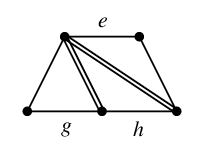
二重辺を消して
$C_e \oplus C_g \oplus C_h=$

$C'$ になりましたね。














