組合せとグラフの理論(塩田)第3回 (2) 名前のついているグラフ その2
(6) 二部グラフ
頂点集合 $V$ が交わりの無い2つの部分集合 $A$, $B$ に分かれ ( $V=A \cup B$, $A \cap B = \emptyset$ )、 $A$ に属する頂点と $B$ に属する頂点の間にしか辺が無いグラフを二部グラフと呼びます。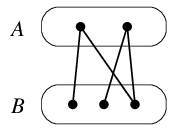
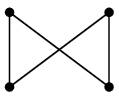
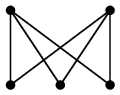
(7) 完全二部グラフ $K_{m,n}$
上の状況で、特に- $|\,A\,|=m$, $|\,B\,|=n$ で、
- $A$ の頂点と $B$ の頂点は必ず隣接する
 |
 |
|
| $K_{2,2}$ | $K_{2,3}$ |
(8) 星グラフ
$K_{1,n}$ のことですが、頂点の配置によって星の形に見えるので星グラフと呼びます。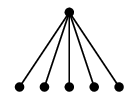 |
$\cong$ | 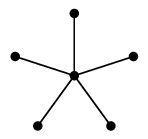 |
||
| $K_{1,5}$ | こう描けば星の形 |
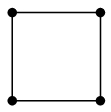
(9) 閉路 $C_n$
$n$ 頂点の、輪の形のグラフです。$n$ 角形の頂点と辺から作ったグラフ、と言っても同じです。 ( 対角線は入れません。)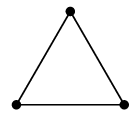 |
 |
|
| $C_3$ | $C_4$ |
(10) 道グラフ $P_n$
$n$ 頂点の、一直線の形のグラフです。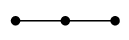 |
 |
|
| $P_3$ | $P_4$ |
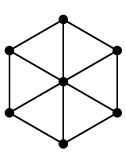
(11) 車輪グラフ $W_n$
$n$ 頂点の、文字通り車輪の形のグラフです。 真ん中にも点があるので $W_n$ は $n-1$ 角形の車輪です。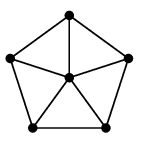 |
 |
|
| $W_6$ は五角形 | $W_7$ は六角形 |
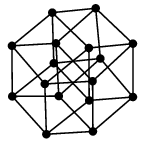
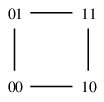
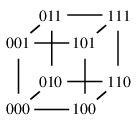
(12) $k$ 次元立方体グラフ $Q_k$
$k$ 次元立方体の頂点と辺から作ったグラフです。 言葉を変えるとこういう定義もできます:- 長さ $k$ のビット列を頂点とする。
- $1$ ビットだけ違うビット列同士を辺で結ぶ。
 |
 |
|
| $Q_2 \cong C_4$ | $Q_3 \cong$ 立方体グラフ |
※ $Q_k$ の中での距離は、符号理論で用いる「ハミング距離」と同じもので、信号の誤り訂正能力に関わる重要な概念です。
形は変えてもいい
以上、「何々の形をした」という書き方をしましたが、同型なグラフは「同じもの」として同じ名前で呼びますので、 頂点の配置は自由に動かして構いません。ここ大事 !たとえば直線の形はしていませんが、次のグラフたちも $P_6$ です: