組合せとグラフの理論(塩田)第3回 (1) 名前のついているグラフ
(1) 完全グラフ $K_n$
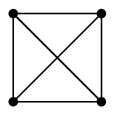
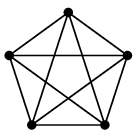
オーダー $n$ で、全ての頂点が互いに隣接している単純無向グラフのこと。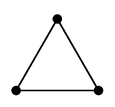 |
 |
 |
||
| $K_3$ | $K_4$ | $K_5$ |
(2) 空グラフ $N_n$
辺を持たない、オーダー $n$ のグラフのこと。「くうグラフ」と読みます。辺集合が空集合、という意味です。 |
 |
|
| $N_3$ | $N_4$ |
(3) 正則グラフ
全ての頂点の次数が等しいグラフのこと。 (これは固有名詞ではありません。たとえば前回の Ex.10 の2つのグラフ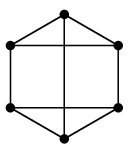
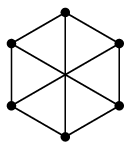
その次数が $r$ のとき、$r$-正則グラフと呼んだり、$r$-正則である、と言ったりします。 例えば、
- $K_n$ は $(n-1)$-正則グラフ
- $N_n$ は $0$-正則グラフ
正則グラフの中でも美しくて有名なのが
(4) ペテルセングラフ(ピーターセングラフ)
オーダー $10$, サイズ $15$, $3$-正則な次のグラフのことです: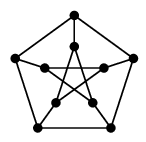
五角形の中に星を描いて内と外をつなげばよいので、自分でも描けるようになりましょう。
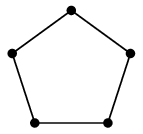 →
→
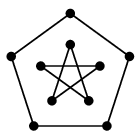 →
→

命題をひとつ
証明 前回の握手補題より例えばペテルセングラフでは $n=10$, $r=3$ で $rn/2=15=$ サイズ、になります。
次も正則グラフの例です:
(5) プラトングラフ
正多面体の頂点と辺から作ったグラフをプラトングラフと呼びます。5種類あります。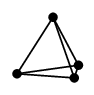 |
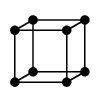 |
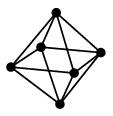 |
||
| 正四面体グラフ | 立方体グラフ | 正八面体グラフ |
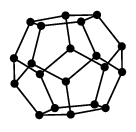 |
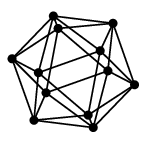 |
|
| 正十二面体グラフ | 正二十面体グラフ |
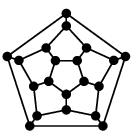
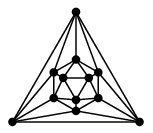
これらのグラフは(同型の意味で)辺を交差させずに 描くことができます:
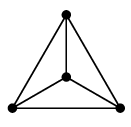 |
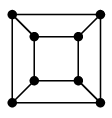 |
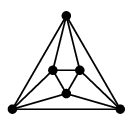 |
||
| 正四面体グラフ | 立方体グラフ | 正八面体グラフ |
 |
 |
|
| 正十二面体グラフ | 正二十面体グラフ |
- 正四面体グラフ、立方体グラフは真上から見た絵をイメージしてください。
- 正八面体グラフ、正十二面体グラフ、正二十面体グラフについては今日の最後に動画でデモをやります。