組合せとグラフの理論(塩田) 2020年度 第13回
今日のテーマ
-
ネットワークフローの勉強をしました、と言って知らないで済まされない「最大フロー・最小カット定理」を今日は勉強します。
1. ネットワークのカット
前回用いた次の記号・設定を今回も継承します。
- $D=(V,A)$ は有向グラフ
- $N=(D, \Psi)$ は $D$ 上のネットワーク
- $N$ の入口は $v$ ひとつだけ
- $N$ の出口は $w$ ひとつだけ
$\newcommand{\ol}[1]{\overline{#1}}$
Def.1
- 頂点集合 $V$ を 2 つの部分集合 $S$, $\ol{S}$ に分けたとき、
$D$ の弧のうち、
$S$ の頂点から $\ol{S}$ の頂点に至るもの全ての集合を $(S,\ol{S})$ と表す。
- 特に、$S$ が入口 $v$ を含み、$\ol{S}$ が出口 $w$ を含むとき、
この形に書ける弧の集合 $K=(S,\ol{S})$ を「( ネットワーク $N$ の ) カット」と呼ぶ。
$K=(S,\ol{S})$ が $N$ のカットであれば $D-K$ は $v$-$w$ 道を含まないことに注意してください。
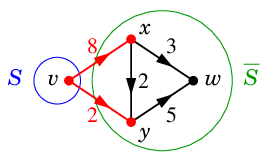
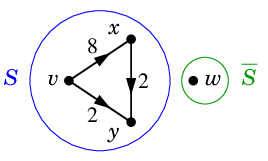
Ex.2 次のネットワークではカットは 4 通りあります。

$S=\{\,v\,\}$, $\ol{S}=\{\,x,y,w\,\}$ のとき、赤い辺たちがカット $K=(S,\ol{S})$ です。
 |
→ |
 |
| $K=(\{\,v\,\},\{\,x,y,w\,\})$ |
|
$D-K$ |
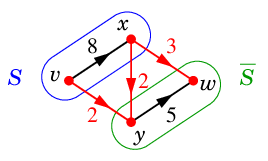
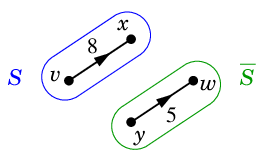
$S=\{\,v,x\,\}$, $\ol{S}=\{\,y,w\,\}$ のときは
 |
→ |
 |
| $K'=(\{\,v,x\,\},\{\,y,w\,\})$ |
|
$D-K'$ |
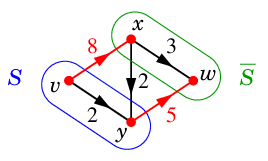
$S=\{\,v,y\,\}$, $\ol{S}=\{\,x,w\,\}$ のときは $D-K''$ に弧 $xy$ が残りますが、
向きが $\ol{S}$ から $S$ へ向かっているのでやはり $v$-$w$ 道はありません。
 |
→ |
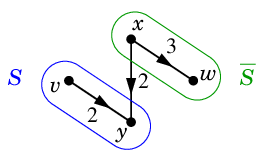 |
| $K''=(\{\,v,y\,\}, \{\,x,w\,\})$ |
|
$D-K''$ |
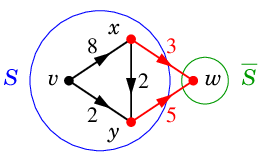
$S=\{\,v,x,y\,\}$, $\ol{S}=\{\,w\,\}$ のとき
 |
→ |
 |
| $K'''=(\{\,v,x,y\,\}, \{\,w\,\})$ |
|
$D-K'''$ |
Rem.3
教科書 p.185 では
「 $D-K$ が $v$-$w$ 道を含まないこと」
を「カット」の定義としていますので、
「Def.1 のカット」は「教科書のカット」のうち極小なもの、
ということになります。
Def.4
- $D$ 上の重み $f$ と、弧の部分集合 $B$ に対し、
$B$ に属する弧の重みの総和を
$\dps{f(B)=\sum_{a \in B} f(a)}$
と表す。
- 特にカット $K=(S,\ol{S})$ に属する弧の容量の総和
$\Psi(K)$ を「カット $K$ の容量」と呼ぶ。
- $N$ のカットの中で容量が最小のものを「$N$ の最小カット」と呼ぶ。
Ex.2 では
\begin{align}
&\Psi(K) =8+2=10 \\
&\Psi(K') =2+2+3=7 \\
&\Psi(K'') =8+5=13 \\
&\Psi(K''')=3+5=8 \\
\end{align}
であり、$N$ の最小カットは $K'$ となります。
フローにカットがどう関わっているかという最初の定理は
Th.5 $N$ の任意のフロー $\varphi$ と任意のカット $K=(S,\ol{S})$ に対し、
( $\varphi$ の値 ) $\leqq \Psi(K)$
が成り立つ。しかも、ここで等号が成立するのは、
- $K=(S,\ol{S})$ の全ての弧 $a$ に対して $\varphi(a)=\Psi(a)$
- $(\ol{S},S)$ の全ての弧 $a$ に対して $\varphi(a)=0$
が成り立つときに限る。
教科書では明らかなように書いてありますが、ちゃんと示しましょう。
Lemma 6 $N$ の任意のフロー $\varphi$ と任意のカット $K=(S,\ol{S})$ に対し、
( $\varphi$ の値 ) $=\varphi((S,\ol{S}))-\varphi((\ol{S},S))$
が成り立つ。
証明 $x \in S$ から出る弧は、$S$ の頂点に至るものと $\ol{S}$ の頂点に至るものに分けられます。従って
$\dps{\mbox{outdeg}(\varphi,x)=\sum_{a=xy,\, y \in S}\varphi(a)+\sum_{a=xy,\, y \in \ol{S}}\varphi(a)}$
この式を全ての $x \in S$ について加えると
$\dps{\sum_{x \in S}\mbox{outdeg}(\varphi,x)=\sum_{a=xy,\, x,y \in S}\varphi(a)+\sum_{a=xy,\, x \in S,\,y \in \ol{S}}\varphi(a)}$
右辺の第 2 項は $\varphi((S,\ol{S}))$ のことですから
$\dps{\sum_{x \in S}\mbox{outdeg}(\varphi,x)=\sum_{a=xy,\, x,y \in S}\varphi(a)+\varphi((S,\ol{S}))}$
となります。向きを逆にして考えると
$\dps{\sum_{x \in S}\mbox{indeg}(\varphi,x)=\sum_{a=yx,\, x,y \in S}\varphi(a)+\varphi((\ol{S},S))}$
この 2 つの式の右辺第 1 項は同じものですから、片々引くと
$\dps{\sum_{x \in S}\left( \mbox{outdeg}(\varphi,x)-\mbox{indeg}(\varphi,x)\right)
=\varphi((S,\ol{S}))-\varphi((\ol{S},S))}$
入口 $v$ 以外の頂点では $\varphi$ の出次数と入次数が釣り合っていますので
左辺 $= \mbox{outdeg}(\varphi,v)-\mbox{indeg}(\varphi,v) =$ ( $\varphi$ の値 )
(証明終)
Th.5 の証明 フローの条件から、各弧 $a$ について $\varphi(a) \leqq \Psi(a)$ が成り立つので
$\varphi((S,\ol{S}))=\varphi(K) \leqq \Psi(K)$
また $\varphi(a) \geqq 0$ が成り立つので
$\varphi((\ol{S},S)) \geqq 0$
従って
L'a 6 により
( フロー $\varphi$ の値 ) $=\varphi((S,\ol{S}))-\varphi((\ol{S},S)) \leqq \Psi(K)$
等号成立条件は以上の議論よりわかります。(証明終)
Th.7 $N$ の或るフロー $\varphi$ と或るカット $K=(S,\ol{S})$ が
( $\varphi$ の値 ) $= \Psi(K)$
を満たせば、$\varphi$ は最大フロー、$K$ は最小カットである。
証明 最大フローのひとつを $\varphi^{\ast}$ 、最小カットのひとつを $K^{\ast}$ とすると、
- $\varphi^{\ast}$ は最大フローゆえ ( $\varphi$ の値 ) $\leqq$ ( $\varphi^{\ast}$ の値 )
- $K^{\ast}$ は最小カットゆえ $\Psi(K^{\ast}) \leqq \Psi(K)$
- Th.5 より ( $\varphi^{\ast}$ の値 ) $\leqq \Psi(K^{\ast})$
これらと仮定をつなぐと、
( $\varphi$ の値 ) $\leqq$ ( $\varphi^{\ast}$ の値 ) $\leqq \Psi(K^{\ast}) \leqq \Psi(K) = $ ( $\varphi$ の値 )
従って全て等号が成り立って、$\varphi$ は最大フロー、$K$ は最小カットとなります。(証明終)
2. 最大フロー・最小カット定理
そしていよいよ、驚くべき定理です。
Th.8(最大フロー・最小カット定理) $N$ の最大フロー $\varphi$ と最小カット $K=(S,\ol{S})$ は必ず
( $\varphi$ の値 ) $= \Psi(K)$
を満たす。すなわち
( 最大フローの値 ) $=$ ( 最小カットの容量 )
が成り立つ。
$N'$ を
前回の「残りを表すネットワーク」とし、次の定理と一緒に証明しましょう。
Th.9(前回の Th.11) ネットワーク $N=(D,\Psi)$ のフロー $\varphi$ が最大フローであることと、
$N'$ が増加道を持たないことが同値である。
Th.9 の証明 $\Rightarrow$) は前回示しました。逆に、$N'$ が増加道を含まないと仮定して、$\varphi$ が最大フローであることを導きましょう。
- $N'$ において入口 $v$ から到達可能な頂点全ての集合を $S$ と置きます。
もちろん $v \in S$ であり、また $N'$ には増加道が無いので $w \not\in S$ ですから $K=(S,\ol{S})$ は $N$ のカットになります。
- $a=xy\in K=(S,\ol{S})$ を任意に取ります。
もし $\Psi'(a) \gt 0$ であれば、$N'$ の中の $v$-$x$ 道と $a=xy$ をつなげば $v$-$y$ 道が作れるので $y \in \ol{S}$ であることに矛盾します。
従って $\Psi'(a) = 0$ でなければなりません。
- $N'$ の作り方から
$\Psi'(a) = \Psi(a) - \varphi(a) + \varphi(a^{-1})$
ですが、フローの条件より $\varphi(a) \leqq \Psi(a)$, $\varphi(a^{-1}) \geqq 0$ ですから、2° により
$\varphi(a) = \Psi(a)$ かつ $\varphi(a^{-1}) = 0$ が言えます。
$a^{-1}$ は $(\ol{S}, S)$ の弧ですから、結局
- $K=(S,\ol{S})$ の全ての弧 $a$ に対して $\varphi(a)=\Psi(a)$
- $(\ol{S},S)$ の全ての弧 $a$ に対して $\varphi(a)=0$
であることがわかりました。
- 3° と Th.5 より ( $\varphi$ の値 ) $= \Psi(K)$ となり、
Th.7 より $\varphi$ は最大フローです。同時に Th.8 も証明できました。(証明終)
Rem.10 最大フロー $\varphi$ に対しては
( $\varphi$ の値 ) $= \Psi(K)$
を満たすカット $K$ が必ず存在します。
もしそのような $K$ が上手く見つかれば、$N'$ を作らなくても $\varphi$ が最大フローであることが言えます。
比較的小さいグラフで最大フローの手計算をするときにはしばしば有効な手段です。
Ex.11(教科書 p.183)
$N$ : 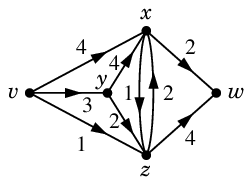
の最大フローは
$\varphi$ : 
でした。
Th.5 の等号条件をヒントに対応する最小カット $K$ を探すと次の赤い弧たちがそうです。
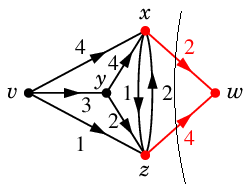
記号で書くと、$S=\{\,v,x,y,z\,\}$, $\ol{S}=\{\,w\,\}$ として $K=(S,\ol{S})$ になります。
また
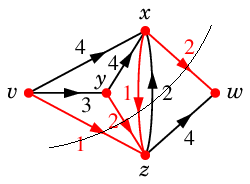
も最小カットです。こちらは $S=\{\,v,x,y\,\}$, $\ol{S}=\{\,w,z\,\}$ の場合です。
Rem.12 「Def.1 のカット」は「教科書のカット」のうち極小なものを指しますので、
Th.7, Th.8 は「教科書のカット」の意味でも成立しています。
3. Menger の定理
最大フロー・最小カット定理は
「どれだけたくさんデータを送れるか」と「どれだけ小さいカットでブロックできるか」が同じ、
という定理でした。
この現象を重みの無いグラフで考えた Menger の定理を紹介します。まず次の問を考えます。
問 $G=(V,E)$ を連結グラフ、$v$, $w$ $\in V$ とするとき、
- 辺を共有しない(辺素な、と言います) $v$-$w$ 道は最大で何本あるか。
- 中間点を共有しない(点素な、と言います) $v$-$w$ 道は最大で何本あるか。
- 有向グラフではどうか。
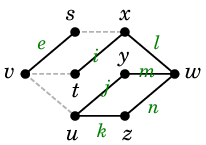
Ex.13 次のグラフで
問 を考えてみましょう。
(黒い記号が頂点、緑の記号が辺です。)
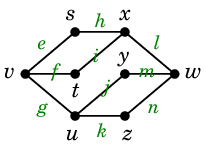
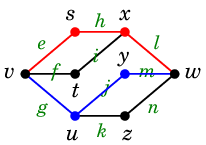
たまたま (1) も (2) も答えは 2 本で、例えば次の図の赤い道と青い道が取れます。
次はブロックする側の定義です。
Def.14
- 辺の部分集合 $F \subseteq E$ が「$vw$-非連結化集合」である、とは、任意の $v$-$w$ 道が $F$ の辺を含むこと。
- 頂点の部分集合 $W \subseteq V$ が「$vw$-分離集合」である、とは、任意の $v$-$w$ 道が $W$ の頂点を中間点として含むこと。
言い換えると
- $\Leftrightarrow$ $G-F$ には $v$-$w$ 道が無いこと。
- $\Leftrightarrow$ $G-W$ には $v$-$w$ 道が無いこと。
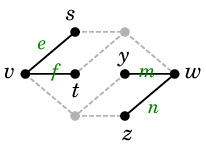
Ex.13 のグラフ

では、例えば $\{\,h,\,i,\,j,\,k\}$, $\{\,h,\,f,\,g\,\}$, $\{\,g,\,\ell\,\}$ はいずれも $vw$-非連結化集合です。
 | |
 | |
 |
| $G-\{\,h,\,i,\,j,\,k\}$ | |
$G-\{\,h,\,f,\,g\,\}$ | |
$G-\{\,g,\,\ell\,\}$ |
また、$\{\,s,\,t,\,u\,\}$ や $\{\,u,\,x\,\}$ は $vw$-分離集合です。
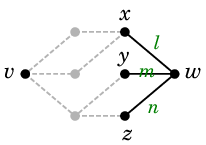 | |
 |
| $G-\{\,s,\,t,\,u\,\}$ | |
$G-\{\,u,\,x\,\}$ |
この例では、$vw$-非連結化集合の辺数の最小値も、
$vw$-分離集合の頂点数の最小値も 2 で
問 の答えに一致していますが、
これが一般にも成り立ちます。
Th.15(辺形の Menger の定理) 辺素な $v$-$w$ 道の最大数は、$vw$-非連結化集合の辺数の最小値に等しい。
Th.16(Menger の定理) 点素な $v$-$w$ 道の最大数は、$vw$-分離集合の頂点数の最小値に等しい。
Th.17(整数性定理) Th.15 は有向グラフでも(辺を弧に読み替えて)成り立つ。
証明 Th.17 は全ての弧の容量が 1 の場合の最大フロー・最小カット定理です。
Th.15 は全ての辺 $e=xy$ を 2 本の逆向きの弧 $xy$, $yx$ に置き換えれば
Th.17 に帰着します。
Th.16 も
Th.17 の応用として証明されます(Bondy-Murty 11章を参照)。
今日は最大フロー・最小カット定理から先に証明しましたが、
歴史的には 1927 年にまず Menger が Menger の定理を証明し、
最大フロー・最小カット定理と辺形の Menger の定理は 1956 年に Ford と Fulkerson によって証明されました。
宿題
- ここから download
- 提出期限:一応来週7月24日を目安に。
- 提出方法:スキャンするか写メを撮るかして、shiota@is.kochi-u.ac.jp 宛に送信してください(@は小文字)。
上手く送信できない人は個別に相談してください。
- 宿題を複数回分まとめて提出されると見落とす危険があります。
多少面倒でも1回分ずつ送信してください。
戻る



















