組合せとグラフの理論（塩田） 2020年度 第12回
今日のテーマ
-
インターネット上ではパケット通信が行われ、データは複数の経路を経由して送られています。
回線にはそれぞれ「回線容量」と言って、単位時間あたりに送受信できるデータ量の上限が決まっています。
この状況下で２つのコンピュータ間で最大でどのくらいのデータが送れるかが問題になります。
このような問題を扱う「ネットワークフロー」を今日は勉強します。
1. フロー（流れ）とは何か？
問 1 例えば次のような単純なコンピュータネットワークを考えましょう。
数字は回線容量を表すとします。
（単位は例えば Mbps = 1秒間に何メガビット送れるか、とします。）
パケット通信を用いて複数の経路を経由してデータが送れるとしたとき、
サーバからクライアントへの最大通信容量はいくらでしょうか？
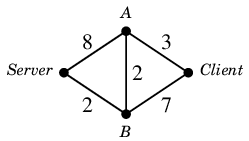
データが流れるとは？
データが安定して流れていると、次の２つが成り立ちます。
- 各回線では、回線容量を超えない範囲でデータが送られている
- 各中継点ではデータの流入量と流出量が釣り合っている
(1) は、川で例えれば流せる上限を超える量の水はあふれてしまうということです。
(2) は、
- 流入量が流出量を超えたらデータが中継点に溜まってしまうし
- 届いてもないデータは送り出せない
ということです。
イマジネーションを働かせてみてください。
問 1 の答え 次のようにデータを送れば 7Mbps の通信容量が実現できます。
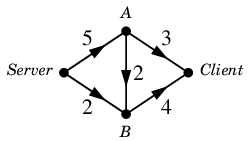
それぞれの回線容量を超えていないことを確かめてください。
また中継点 $A$ では流入量 $5$ と 流出量 $2+3$ が釣り合っていますし、
中継点 $B$ では流入量 $2+2$ と 流出量 $4$ が釣り合っていますね。
中継点で流入量と流出量が釣り合っているので、
サーバからの送信量 $5+2=7$ がクライアントの受信量 $3+4=7$ に一致しています。
2. 定式化
1. の状況をグラフ理論的に表現しましょう。
Def.3
- 重み付き有向グラフは次のように表す。
$N=(D, \Psi)$
- $D=(V,A)$ は有向グラフ
- 弧 $a \in A$ に対して $\Psi(a)$ は $a$ の重みを表す。 ただし $\Psi(a) \geqq 0$ とする。
- 重み付き有向グラフにおいては入出次数は重みの和で定義する：
- $\mbox{indeg}(\Psi,x)=$ $x$ に入る弧 $a$ の重みの和
- $\mbox{outdeg}(\Psi,x)=$ $x$ から出る弧 $a$ の重みの和
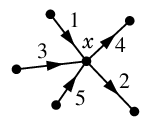なら
$\left\{
\begin{array}{ll}
\mbox{indeg}(\Psi,x)\!\!&\!\!=1+3+5=9 \\
\mbox{outdeg}(\Psi,x)\!\!&\!\!=4+2=6 \\
\end{array}
\right.$ です。
$\Psi$ はギリシャ文字のプサイです。
Def.4
- 連結な重み付き有向グラフを特に「ネットワーク」と呼ぶ。
- 「ネットワーク」という言葉遣いをするときは、重み $\Psi(a)$ のことを「$a$ の容量」と呼ぶ。
- $\mbox{indeg}(\Psi,x)=0$ となる頂点を「入口」、$\mbox{outdeg}(\Psi,x)=0$ となる頂点を「出口」と呼ぶ。
※ 以下簡単のため、入口は $v$ １個、出口は $w$ １個しかない、とします。
Ex.5（教科書 p.183）
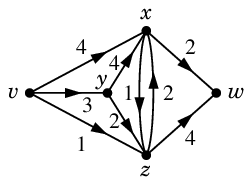
このネットワークでは $v$ が入口、$w$ が出口です。
次は「流れ」を式で表現しましょう。
Def.6 $D$ 上のもうひとつの重み $\varphi$
(ファイ) が
ネットワーク $N$ の「フロー」であるとは、
- 全ての弧 $a \in A$ について $0 \leqq \varphi(a) \leqq \Psi(a)$ であり、
- 入口 $v$, 出口 $w$ 以外の全ての頂点 $x$ について
$\mbox{indeg}(\varphi,x)=\mbox{outdeg}(\varphi,x)$ ... 2022.7.2 訂正
が成り立つこと。
Def.7 フロー $\varphi$ では
入口 $v$ からの流出量 $\mbox{outdeg}(\varphi,v)=$ 出口 $w$ への流入量 $\mbox{indeg}(\varphi,w)$ ... 2022.7.2 訂正
が成り立つ。この値を「フロー $\varphi$ の値」と呼ぶ。
Def.8 ネットワーク $N$ を与えたとき、フローの値が最大となるフローを「最大フロー」と呼ぶ。
コンピュータネットワークの場合に役割を整理しておきましょう：
- ネットワークの設定は $N=(D,\Psi)$
- 入口 $v$ はサーバ、出口 $w$ はクライアント
- フロー $\varphi$ はデータが安定して流れている状態
- $\Psi(a)$ は回線 $a$ の容量
- $\varphi(a)$ は回線 $a$ を流れている情報量
- 最大フローは最大通信容量が達成できている状態
- 最大フローの「フローの値」は最大通信容量
「フロー」と「フローの値」をごっちゃにする人がよくいます。間違えないように。
ここまでのおさらい Ex.5 のネットワーク
において、
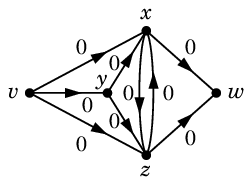
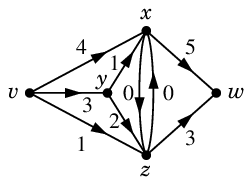
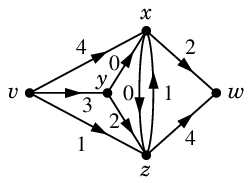
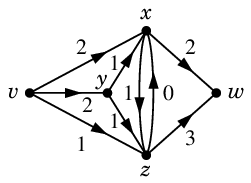
次のうちフローの条件を満たすのはどれ？
答え
フローの条件を満たしているのは (1) と (4) です。(1) は何も流れていない状態を表し、ゼロフローと呼びます。
(2) は $xw$ の重みが容量を超えてしまっています。
(3) は入次数と出次数が中継点の $x$, $y$, $z$ で合っていません。
3. 最大フローアルゴリズム
最大フローを求めるアルゴリズムのアイデアは割とシンプルです。
アイデア 問 1 のネットワーク
$\varphi$ :
では、例えば次のフロー $\varphi$ は簡単に思いつきます。
$\varphi$ :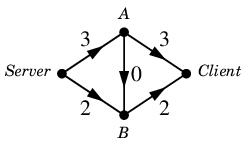 
まだ回線容量には余裕があって、あとどの位容量に余裕があるかを書き出すと
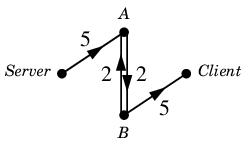
となります。この「残りのネットワーク」の中ではさらに次の
道の形のフロー $\varepsilon$ が見つかります。
$\varepsilon$ :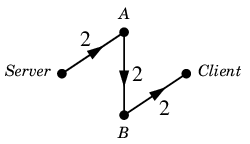 
各弧で容量を足して
新 $\varphi=\varphi + \varepsilon$
とおくと、これは最大フローになっています。
新 $\varphi$ :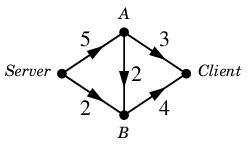 
※ このように
- 各回線の容量の残りはいくつか
- その「残り」の中でどれだけフローの値を増やせるか
を考えます。
Def.9（「残り」の表し方） ネットワーク $N=(D,\Psi)$ のフロー $\varphi$ があたえられたとき、
その残りを表すネットワーク $N'=(D,\Psi')$ を次で定める。
$\left\{
\begin{array}{l}
\Psi'(a)=\Psi(a)-\varphi(a) \\
\Psi'(a^{-1})=\Psi(a^{-1})+\varphi(a) \\
\end{array}
\right.$
$\forall a \in A$
ただし $a^{-1}$ は $a$ と逆向きの弧を表す。
$a^{-1}$ を考える理由は後述します。
Def.10（ $\varepsilon$ の見つけ方） 上記の $N'$ の中で、
正の容量を持つ弧からなる $v$-$w$ 道 $P$ が存在するとき、
$P$ 上の弧の「残りの容量」の最小値を
$\dps{m=\min_{a \in P} \Psi'(a)}$
とおいて、$P$ 上の弧に重み $m$ を与えたフローを $\varepsilon$ とする：
$\varepsilon(a)=
\left\{
\begin{array}{ll}
m & a \mbox{ が } P \mbox{ 上の弧のとき } \\
0 & \mbox{ otherwise} \\
\end{array}
\right.$
$\varepsilon$ を「増加道（フロー増加道）」と呼ぶ。
アイデア では
$P$ :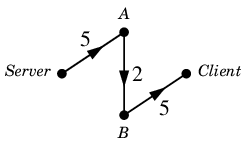 
が $N'$ の中の $v$-$w$ 道であり、
真ん中が一番細いのでそれに太さを揃えたのが $\varepsilon$ です。
$\varepsilon$ が「増加道」であれば
新 $\varphi=\varphi + \varepsilon$
は $\varphi$ よりフローの値が大きいフローとなりますが、
もっと強く次が言えます。
Th.11 ネットワーク $N=(D,\Psi)$ のフロー $\varphi$ が最大フローであることと、
$N'$ が増加道を持たないことが同値である。
証明は次回やります。この定理により
Algorithm 12（最大フローアルゴリズム）
- 入力：ネットワーク $N$
- 出力：$N$ の最大フロー $\varphi$
$\varphi=$ 適当なフロー
while True:
$N'=$ (
Def.9 のネットワーク )
if $N'$ に $v$-$w$ 道 $P$ が存在：
$\varepsilon=$ (
Def.10 の増加道 )
新 $\varphi=\varphi + \varepsilon$
else:
$\varphi$ を出力して終了
- $v$-$w$ 道 $P$ を見つけるには、例えば $N'$ で $v$ を根とする（弧の向きに沿った）幅優先探索を実行します。
- プログラムを組むときは、$\varphi$ の初期値は
$\varphi=$ ゼロフロー $=$ 何も流れていない状態
としますが、人間は賢いのである程度のフローを見つけてから始めます。
4. 最大フローアルゴリズム実行例
Ex.5 のネットワーク
$N$ :
の最大フローを
Alg.12 に従って求めてみましょう。
まず適当に（容量・入出次数に気を付けて）次のフロー $\varphi$ を見つけておきます。
$\varphi$ :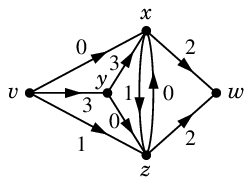 
Def.9 に従って $N'$ を作ります。
(簡単のため容量 $0$ の弧は省略してあります。)
この作業が一番煩雑なので丁寧に見てください。
$N'$ :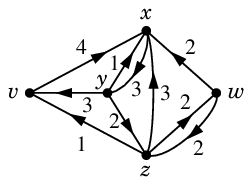 
$N'$ の中で弧の向きに沿った幅優先探索を実行すると、次の赤い $v$-$w$ 道 $P$ が見つかります。
$P$ :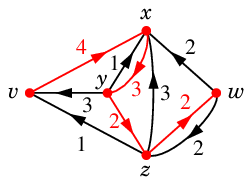 
$P$ 上の弧の「残りの容量」の最小値は $2$ なので、
Def.10 の増加道 $\varepsilon$ は
次のようになります。
$\varepsilon$ :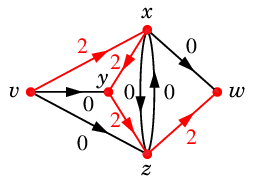 
$\varphi$ と $\varepsilon$ の重みを足し合わせて新しい $\varphi$ とします。
($yx$ と $xy$ は逆向きなので、重み $3$ と $2$ を相殺して $yx$ の重みを $1$ にします。)
$\varphi$ は
, $\varepsilon$ は
$\downarrow$
新 $\varphi$ : 
Def.9 に戻って $N'$ を更新します。
$N'$ :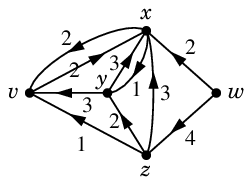 
$N'$ には $v$-$w$ 道が無くなりましたので $\varphi$ が最大フローになりました。
Rem.13 弧の容量が全て整数値の場合（実用ではたいていそうです）、
Alg.12 のループ回数は多くとも容量の最大値以下ですから、
$P$ をみつけるのに幅優先探索を使えばこのアルゴリズムは高速に実行できます。
5. $a^{-1}$ を考える理由
次のネットワークにおいて
$N$ :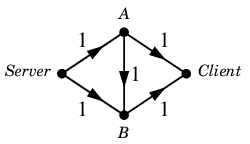 
初めにこのようなフロー $\varphi$ を見つけたとしましょう。
$\varphi$ :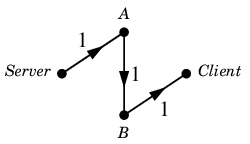 
このとき $a^{-1}$ を考えずに $N'$ を作ってしまうと
失敗 $N'$ :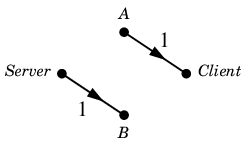 
となって $N'$ には $v$-$w$ 道が無いので増加道が作れません。
ところが $a^{-1}$ を考えて $N'$ を作れば
本当の $N'$ :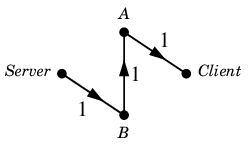 
となり、次のように増加道 $\varepsilon$ が見つかります。
$\varepsilon$ :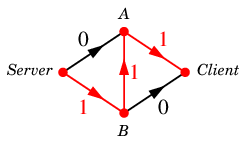 
新 $\varphi=\varphi+\varepsilon$ は
新 $\varphi$ :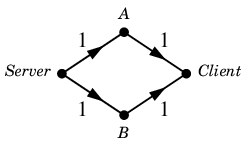 
となって最大フローになります。
最初の $\varphi$ では真ん中の回線を使っていましたが、
使わなかった方が通信容量が増えた訳で
「使ってみたけどやめた」
というときのために $a^{-1}$ を登録してあるのです。
6. 無向グラフの場合
無向グラフはどの辺も双方向に通信可能なネットワークと考えられ、
最大フローアルゴリズムを実行することができます（ただし入口・出口が自動的には決まりませんが）。
例えば完全グラフ（全ての辺の容量１）では次のような最大フローが得られます。
→ 
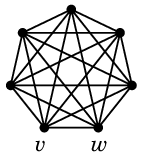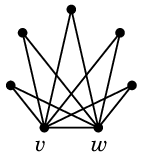
頂点数を増やすとこんな絵が描けます。
デモ動画
mp4 が再生可能なブラウザでご覧ください。
宿題
- ここから download
- 提出期限：一応次回を目安に。
- 提出方法：スキャンするか写メを撮るかして、shiota＠is.kochi-u.ac.jp 宛に送信してください（＠は小文字）。
上手く送信できない人は個別に相談してください。
- 宿題を複数回分まとめて提出されると見落とす危険があります。
多少面倒でも１回分ずつ送信してください。
戻る
