組合せとグラフの理論(塩田) 2020年度 第9回
今日のテーマ
-
グラフはいつも平面の上に描いているのに「何を今さら」と思うかもしれませんが、
例えば図の $K_4$ では $ux$ と $vw$ は本当は交点を持っていないのに、
初学者はそこに交点があるように誤解してしまいます。
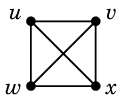 そこで、交点を持たない辺同士は交わらないように描画したいな、というのが平面性の考え方です。
そこで、交点を持たない辺同士は交わらないように描画したいな、というのが平面性の考え方です。
1. 平面性の定義
Def.1 平面上に、辺の交差無く描かれているグラフを「平面グラフ」と呼ぶ。
Def.2 平面グラフと同型なグラフを「平面的グラフ」と呼ぶ。
「的」の字があるか無いかはどこが違うのかと言うと
Ex.3 $K_4$ はこう描くと辺が交差していますので平面グラフではありません。
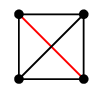
しかし、交差している辺の片方を「外」に出せば、交差を無くすことができます。
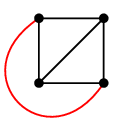
このグラフは平面グラフです。
従ってこの平面グラフと同型な $K_4$ は平面
的グラフ、ということになります。
Ex.4 $K_{2,n}$ も次のように描けば平面的であることがわかります。
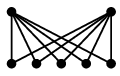 →
→
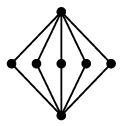
Ex.5 第3回に見たようにプラトングラフは全て平面的です。
 |
|
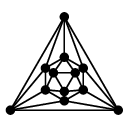 |
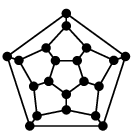
| 正十二面体グラフ |
|
正二十面体グラフ |
Rem.6
- 「平面グラフか否か」は描画に依存する性質です。
ここ大事!
- これに対し「平面的グラフか否か」は同型で保たれる性質です。
- 「平面的」とは「上手に絵を描けば辺の交差を無くせる」ということです。
Rem.7 電気回路を表すグラフが平面的であれば、
導線を交差させないデザインが可能ですので、
1層の基盤で実現することができ
コストが抑えられます。
とてもいいことです。
2. クラトフスキーの定理
平面性の判定条件については、クラトフスキーの定理、という有名な定理があります。
まずは簡単な命題から。
Prop.8 $H$ をグラフ $G$ の部分グラフとする。このとき
- □ が平面的 $\Rightarrow$ □ も平面的。
- □ が非平面的 $\Rightarrow$ □ 非平面的。
□ には $G$ と $H$ のどちらが入るでしょうか。
答えは自分で考えてから
- $G$ が平面的 $\Rightarrow$ $H$ も平面的。
- $H$ が非平面的 $\Rightarrow$ $G$ も非平面的。
証明 (1) $G$ は辺の交差無く描けますので、$H$ はそこからいくつかの頂点と辺を消せば宜しい。
(2) は (1) の対偶です。( 一部分である $H$ すら辺の交差無く描けないのに、 $G$ 全体はムリ、って話。)
※ 辺が多いほど描ける場所が減ってきて、交差ができ易くなる、という感覚が大事です。
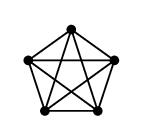
さて、平面性の要
(かなめ)となるのは、次の 2 つのグラフです。
 |
|
 |
$K_5$ |
|
$K_{3,3}$ |
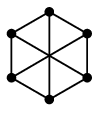
Th.9 $K_5$ は非平面的である。
証明 頑張って辺の交差無く描いてみましょう。
- $K_5$ の部分グラフ $C_5$ はねじらずに描かねばなりません。
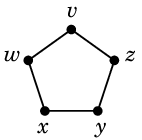
- 辺 $wz$ をこの5角形の内側に描く場合を考えます。(後の Th.14 より内側に描く場合のみ考えればよいことがわかります。)
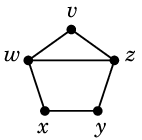
- すると辺 $vx$, $vy$ は5角形の外側に描かざるを得ません
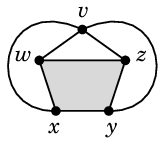 または
または
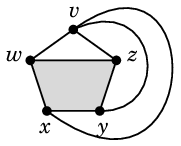 またはその逆
またはその逆
- 残る 2 本の辺 $wy$, $xz$ は色付きの4角形の領域に描かざるを得ませんが、交差させずに描くことは不可能です。
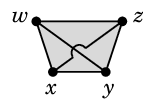
(証明終)
Th.10 $K_{3,3}$ は非平面的である。
証明 Th.9 の証明と同様に、
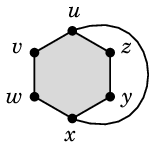
ここまで描くと残る 2 本の辺 $vy$, $wz$ は6角形の内側に描かざるを得ず、
交差させずに描くことは不可能です。
(証明終)
Th.11(クラトフスキー) グラフ $G$ について次は同値である。
- $G$ は平面的である。
- $G$ のいかなる部分グラフを縮約しても、$K_5$ や $K_{3,3}$ にはならない。
- $G$ のいかなる部分グラフも、$K_5$ や $K_{3,3}$ に位相同型ではない。
ただし位相同型とは、次の図のように次数 2 の部分を描き替えると同型になること。
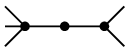 →
→

証明はとても長いので省略します。
Ex.12 ペテルセングラフ は非平面的である。
クラトフスキーの定理を用いた証明は
プリント の第1, 第2の証明を見てください。
Rem.13 Th.11 は定理としては美しいのですが、
「全ての部分グラフ」は膨大な個数存在しますのでプログラミングには使えません。
塩田のグラフ描画ツールでは計算量 $O(n^4)$ の平面性判定アルゴリズムを実装してあります ( $n$ は頂点数 )。
3. オイラーの公式
平面グラフに「面」を定義するために、ひとつ定理を書きます。
Th.14 グラフが平面上に辺の交差無く描けることと、
球面上に辺の交差無く描けることは同値である。
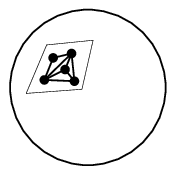
証明 $\Rightarrow$ ) 小さな紙に描いておいて球面に張り付ければよい。
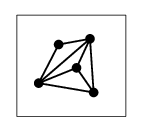 →
→
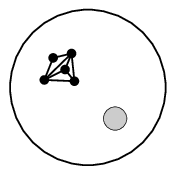
$\Leftarrow$ ) グラフを避けて球面に穴をあけて、穴を広げればよい。
 →
→
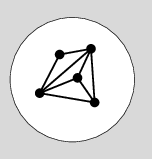
(証明終)
Rem.15
- Th9-10 の証明は、球面上に描くと思えば内側外側の区別が不要になります。
- プラトングラフの平面グラフとしての描画 ( Ex.5 ) は、正多面体の面のひとつに穴をあけて広げたものです。
Def.16 平面グラフの、辺で区切られた各領域を「面」と呼ぶ。
一番外側も 1 つの面と考える。
※ 球面上に描けば「一番外側」という区別がなくなるので、その面も同等に扱う訳です。
※ 「面」と言うときは
辺が交差していないことが前提 です。
ここ特に大事!!
Th.17(オイラーの公式) $G$ を連結な平面グラフ、$n$, $m$, $f$ をその頂点数、辺数、面の個数とする。
このとき
$n - m + f = 2$
Ex.18 プラトングラフで確かめてみましょう。
答え
|
$n$ |
$m$ |
$f$ |
$n-m+f$ |
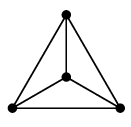
| 正四面体グラフ | 4 | 6 | 4 | 2 |
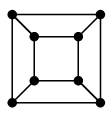
| 立方体グラフ | 8 | 12 | 6 | 2 |
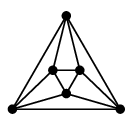
| 正八面体グラフ | 6 | 12 | 8 | 2 |
| 正十二面体グラフ | 20 | 30 | 12 | 2 |
| 正二十面体グラフ | 12 | 30 | 20 | 2 |
$n$, $m$, $f$ の値が対称に並んでいる理由は次回勉強します。
Th.17 の証明 $m$ についての帰納法を用います。
- $m$ が一番少ないのは $G$ が木のときで $m=n-1$ であり、面は外側のひとつだけなので $f=1$。
よって $n-m+f = n - (n-1) + 1= 2$ となって成り立ちます。
- $G$ が木でないときは、$G$ 内の閉路 $C$ と、$C$ 上の辺 $e$ を 1 本選んで
$G'=G-e$
を考えます。$G'$ は $G$ の部分グラフゆえ平面グラフで、そのパラメータを $n'$, $m'$, $f'$ とおくと
- 頂点は消していないので $n'=n$
- 辺は 1 本除去したので $m'=m-1$
- $e$ の表側の 2 つの面が 1 つにつながったので $f'=f-1$
よって
$n-m+f=n'-(m'+1)+(f'+1)=n'-m'+f'=2$.
ここで $G'$ に帰納法の仮定を使いました。(証明終)
Cor.19 $G$ を連結な平面的単純グラフ、$n$, $m$ をその頂点数、辺数とする。
このとき次が成り立つ。
- $m \leqq 3n-6$.
- $G$ が3角形を含まなければ $m \leqq 2n-4$.
- 次数 5 以下の頂点が必ずある。
証明 (1) 1 つの面は 3 本以上の辺で囲まれていて、1 本の辺は 2 つの面で使われますので、
$3f \leq 2m$
が成り立ちます。従って
$2=n-m+f \leqq n -m + \frac{2}{3}m = n- \frac{1}{3}m$.
(2) 3角形を含まなければ 1 つの面は 4 本以上の辺で囲まれますので、今度は
$4f \leq 2m$
となり
$2=n-m+f \leqq n -m + \frac{1}{2}m = n- \frac{1}{2}m$.
(3) もし全ての頂点の次数が 6 以上であれば
$2m=$ 次数の和 $\geqq 6n$
となって (1) に矛盾します。
(証明終)
※ プリントの「第3の証明」はこの
Cor.19 と同じパターンを使ったものです。
※ Cor.19 の条件は必要条件でしかなく、
$m \leqq 3n - 6$ が成り立ったからと言って平面的であるとは言えません。
ここも大事!
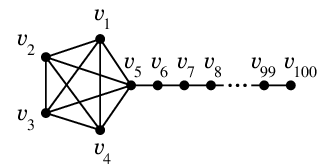
$n=100$, $m=105$ なので $m \leqq 3n -6$ は成り立つが非平面的な例 ( $K_5$ を含むので非平面的 )
4. 交差数 $\mbox{cr}(G)$ と厚さ $\mbox{t}(G)$
非平面的グラフについて、それがどのくらい平面的から遠いかを数で表しましょう。
Def.20
- $G$ を平面上に描くときに生じる辺の交差の最小数を「$G$ の交差数」と呼び、$\mbox{cr}(G)$ と表す。
- $G$ ( の辺 ) をいくつかの平面的な部分グラフに分ける最小数を「$G$ の厚さ」と呼び、$\mbox{t}(G)$ と表す。
Rem.21
- $G$ が平面的 $\Leftrightarrow$ $\mbox{cr}(G)=0$ $\Leftrightarrow$ $\mbox{t}(G)=1$
- $K_5$ は非平面的ですから交差数は 1 以上ですが、図のように交差1 つで描画できますので $\mbox{cr}(K_5)=1$ です。
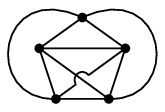
- また $K_5$ は次のように 2 つの平面的部分グラフに分けられますので $\mbox{t}(K_5)=2$ です。
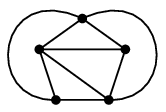
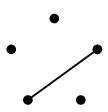
- この例のように、交差する辺を 1 つずつ別の部分グラフに割り当てることで
$\mbox{t}(G) \leqq \mbox{cr}(G)+1$ であることがわかります。
※ 交差数は立体交差をイメージすればよく、
厚さの方は「電気回路が何層で設計できるか」と想像すれば覚えられるでしょう。
デモ動画
mp4 が再生可能なブラウザでご覧ください。
宿題
- ここから download
- 提出期限:急がなくていいですが、一応次回を目安に。
- 提出方法:スキャンするか写メを撮るかして、shiota@is.kochi-u.ac.jp 宛に送信してください(@は小文字)。
上手く送信できない人は個別に相談してください。
- 宿題を複数回分まとめて提出されると見落とす危険があります。
多少面倒でも1回分ずつ送信してください。
... 現在3科目担当していて合計130名程度の受講生がおります。
課題チェックの作業量をちょっと想像してみてください。
戻る





 または
または
 またはその逆
またはその逆


 →
→

 →
→




 →
→



 →
→



