今日はこの授業でどんなことをやるのか、というお話です。

はじめに

1. 「組合せとグラフの理論」という講義名ですが、グラフ理論を主にやります。
2. 新型コロナウイルス対策で始めのうちは Web 教材を提示しますが、対面授業に戻ったら板書でやります。 写メで撮って楽をしてはいけません。 ノートを取るという作業を通じて脳を動かすことが大事です。
3. 毎回宿題を出します。宿題と試験を合わせて成績を付けます。
4. オリジナルのツールでデモをやります。お得な授業です。

グラフ理論の始まり：ケーニヒスベルクの７つの橋渡り

　グラフ理論で扱う「グラフ」とはどんなものか、を理解してもらうために、グラフ理論が生まれたエピソードを紹介します。

　18世紀初め、ロシア、ケーニヒスベルクの町で「７つの橋渡り」という遊びが流行りました。 プルーゲル川の両岸と２つの中洲に架かる７つの橋を丁度１回ずつ渡って散歩できるか、というクイズです。

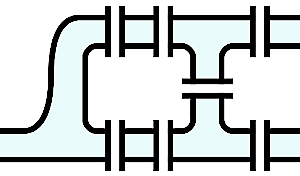
誰ひとりうまくいきません。もし不可能なら、不可能であることを証明してもらいたい、ということでオイラー先生に HELP が掛かりました。 　オイラー先生は

• 岸や中洲を点
• 橋を辺

として地図を抽象化することを思い付きました。（面である岸や中洲を点にしてしまうというこの大胆な発想 !!）　 するとこんな絵が得られます：
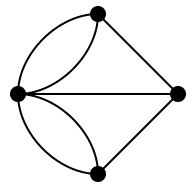
上下の点が岸、左右の点が中州を表しています。ここのところ、よく理解してください。 このようにモノのつながりを表現した図形（と言うか構造）を「グラフ」と呼びます。

　さて、橋渡りのクイズは、このグラフで一筆描きができるか、という問題に言い換えることができます。 そしてオイラー先生は「一筆描きの定理」を証明することによって、橋渡りが不可能であることを証明しました： 橋渡りのグラフでは４つの点の次数が 5, 3, 3, 3 ですので一筆描きができないことがわかります。

四色定理

　グラフ理論を用いて解決した問題をもうひとつ紹介します。

　色刷りの地図を作る印刷業者たちは、経験的に次の事実を知っていました： 地図の塗り分けは次のようにしてグラフで表現できます。例えば中部地方周辺の地図を考えましょう。 先ず、各都府県にひとつずつ点を描きます。 次に、隣り合う都府県について、その点同士を辺で結びます。すると、「隣り合う」というつながりを表現したグラフができます。 このグラフの点に番号を割り振って、隣り合う点同士の番号が必ず異なるようにします。例えば次のように割り振れば番号は４つで足ります。 この番号を色の番号だと思って各都府県に色を塗れば、地図の塗り分けができます。 　四色問題が学会に提唱されたのは1852年ですが、証明されたのはそれから124年後の1976年。 アッペルとハーケンが「基本的な地図」を約2000個に分類することで解決しました。 コンピュータを用いた証明の魁（さきがけ）でもあります。

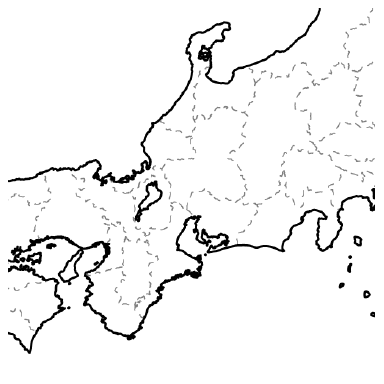
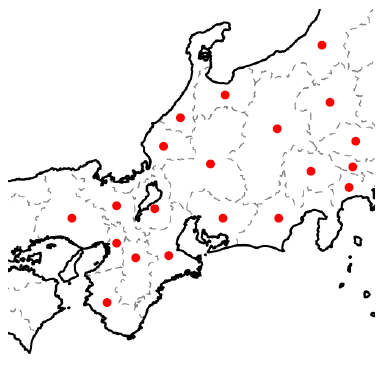
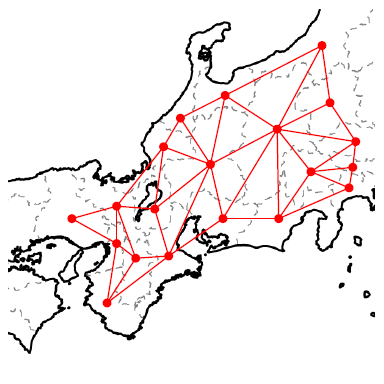
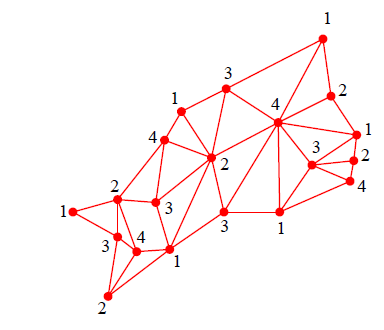
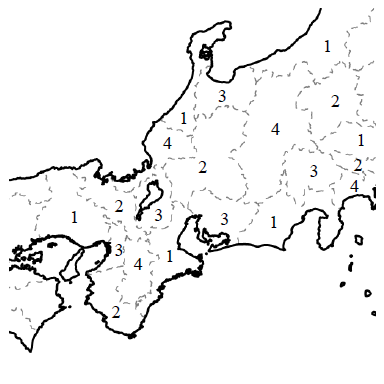
フリー素材提供：白地図専門店

グラフ理論の目標

　「７つの橋渡り」や「地図の塗り分け」のように、モノのつながり方に関係する問題を

• グラフとして表現し、
• グラフ理論の定理やグラフ・アルゴリズムを用いて解く

ことがグラフ理論の大きな目標のひとつです。

　この授業では次のような問題を扱ってゆきます。

• 探索 ... データ構造の基本的なアルゴリズム
• 一筆描き
• 最短路問題 ... カーナビや 高速道路のルート検索 で必須のアルゴリズム
• 巡回セールスマン問題 ... 全ての顧客を訪問する最短コースを求める問題
• 郵便配達員問題 ... 全ての道路を通る最短コースを求める問題
• 彩色問題 ... 地図の塗り分け、スケジュール調整、レジスタの割り付け等に応用される
• 平面性の問題 ... 電子回路設計に応用される
• 連結度 ... ネットワークの安全性に関わる問題
• ネットワーク・フロー ... ネットワークの通信容量等を測る問題
• マッチング ... 相性のいいペアを沢山作る問題 （入退院サポートシステムへの応用例）etc.

宿題

• ここから download
• 提出期限：こんなご時世ですので、急がなくていいです。
• 提出方法：スキャンするか写メを撮るかして、shiota＠is.kochi-u.ac.jp 宛に送信してください（＠は小文字）。 できなければ後日紙で提出しても構いません。 上手く送れない人はメールで連絡してください。
• 宿題を複数回分まとめて提出されると見落とす危険があります。 多少面倒でも１回分ずつ送信してください。 ... 現在３科目担当していて合計130名程度の受講生がおります。 課題チェックの作業量をちょっと想像してみてください。