応用数学（塩田）2022年度

応用数学第12回 (6)　畳み込み

前へ / 戻る / 次へ

$\newcommand{\LT}{\mathscr{L}}$

畳み込み

　畳み込み ( 合成積、convolution ) の定義は、フーリエ変換のときとは、関数の定義域や積分区間が違っています：

Def.13　

$t \geqq 0$ で定義されたふたつの関数

$f(t)$ ,

$g(t)$ に対して

$\dps{(f \ast g)(t) = \int_{0}^{t} f(t-x)g(x)dx}$ を「

$f$ と

$g$ の畳み込み」と呼ぶ。

※　ただし「

$f(t)$ ,

$g(t)$ の値は

$t \lt 0$ では

$0$ 」だと解釈すれば

$\dps{(f \ast g)(t) = \int_{-\infty}^{\infty} f(t-x)g(x)dx}$ とも書けますので、これならフーリエ変換のときと同じものになります。

　そして、フーリエ変換のときと同様に次が言えます：

Th.14　

$\LT(f \ast g)=\LT(f) \times \LT(g)$ .

証明　

$\begin{align} \LT(f)(s) \times \LT(g)(s) &=\int_0^{\infty} f(u)e^{-su}du \times \int_0^{\infty} g(v)e^{-sv}dv \\ &=\int_0^{\infty} \int_0^{\infty} f(u)g(v)e^{-s(u+v)}du dv \\ \end{align}$ ここで

$t=u+v$ ,

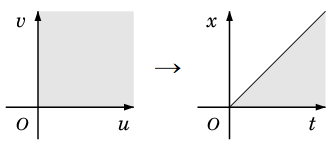
$x=v$ と変数変換すると、積分領域は

$\{\,(u,v)\,|\,u,\,v \geqq 0\,\}$ から

$\{\,(t,x)\,|\,t \geqq 0$ ,

$0 \leqq x \leqq t\,\}$ に写り、

ヤコビ行列式は

$\dps{ \left|\,\frac{\partial(u, v)}{\partial(t,x)}\,\right| =\left| \begin{array}{rr} 1 & -1 \\ 0 & 1 \\ \end{array} \right| =1 }$ ゆえ右辺

$\dps{=\int_0^{\infty} \left(\int_0^{t} f(t-x)g(x)dx\right)e^{-st}dt =\LT(f \ast g)(s). }$ (証明終)

前へ / 戻る / 次へ