応用数学 第9回 (4) フーリエ展開の例
偶関数・奇関数のフーリエ係数
Rem.9 $f(x)$ のフーリエ係数について
- $f(x)$ が偶関数ならば $b_n=0$ ( $\forall n \geqq 1$ )
- $f(x)$ が奇関数ならば $a_n=0$ ( $\forall n \geqq 0$ )
が成り立ちます。
ただし
- $f(x)$ が偶関数とは「 $f(-x)=\ \ \ f(x)$, $\forall x$ 」が成り立つこと
- $f(x)$ が奇関数とは「 $f(-x)=-f(x)$, $\forall x$ 」が成り立つこと
で、
Th.4 $(\star)$ で $t=-x$ と置換すれば示せます。
例
Ex.10 $f(x)$ を、$x$ ( $-\pi \lt x \leqq \pi$ ) を周期 $2\pi$ で貼り合わせた関数
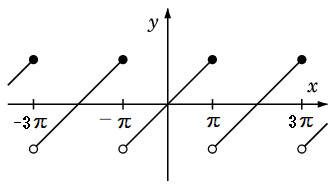
とするとき
\begin{align}
f(x)
&=2\,\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}\sin(nx) \\
&=2 \left(\frac{\sin(x)}{1}-\frac{\sin(2x)}{2}+\frac{\sin(3x)}{3}-\frac{\sin(4x)}{4}+\cdots\right) \\
\end{align}
$\mbox{if }\ x \neq (2k+1)\pi$
証明 $f(x)$ は不連続点を除いては奇関数ゆえ $\forall a_n=0$ であり、
\begin{align}
b_n
&= \frac{1}{\pi}\int_{-\pi}^{\pi}x\sin(nx)dx \\
&= \frac{1}{\pi}\Big\{\left[-\frac{1}{n}x\cos(nx)\right]_{-\pi}^{\pi}
+\frac{1}{n}\int_{-\pi}^{\pi}\cos(nx)dx\Big\}
=2\frac{(-1)^{n+1}}{n} \\
\end{align}
(証明終)
なお $x=(2k+1)\pi$ では右辺 $=0$ ですが、
$\dps{\frac{1}{2}(f(x-0)+f(x+0))= \frac{1}{2}(\pi + (-\pi)) =0}$
となって
Th.8 (2) のとおりになっています。
Cor.11 ( ライプニッツの級数 )
$\dps{1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots=\frac{\pi}{4}}$
この式は
Ex.10 で $\dps{x=\frac{\pi}{2}}$ とおけば得られます。
※ フーリエ展開はこのような級数和の公式をたくさん産み出します。
次の例
Ex.12 $f(x)$ を、$\pi-|\,x\,|$ ( $-\pi \lt x \leqq \pi$ ) を周期 $2\pi$ で貼り合わせた関数

とするとき
\begin{align}
f(x)
&=\frac{\pi}{2}+\frac{4}{\pi}\sum_{\mbox{$n:$奇数$\geqq 1$}}\frac{1}{n^2}\cos(nx) \\
&=\frac{\pi}{2}+\frac{4}{\pi}\left(\frac{\cos(x)}{1^2}+\frac{\cos(3x)}{3^2}+\frac{\cos(5x)}{5^2}\cdots\right) \\
\end{align}
証明 $f(x)$ は偶関数ゆえ $\forall\, b_n=0$ であり、
\begin{align}
a_0
&= \frac{1}{\pi} \times 2 \int_{0}^{\pi} (\pi-x) dx
= \frac{1}{\pi} \times 2 \frac{\pi^2}{2} = \pi , \\
a_n
&= \frac{1}{\pi}\times 2\int_{0}^{\pi}(\pi-x)\cos(nx)dx \\
&= \frac{2}{\pi}\Big\{\left[\frac{1}{n}(\pi-x)\sin(nx)\right]_{0}^{\pi}
+\frac{1}{n}\int_{0}^{\pi}\sin(nx)dx\Big\} \\
&= \frac{2}{\pi}\left\{0+\frac{1}{n}\left[-\frac{1}{n}\cos(nx)\right]_{0}^{\pi}\right\}
=\left\{
\begin{array}{ll}
\displaystyle{\frac{4}{\pi n^2}} & n: \mbox{奇数} \\
0 & n: \mbox{偶数} \geqq 2 \\
\end{array}
\right.\\
\end{align}
(証明終)
Cor.13
- $\dps{1+\frac{1}{3^2}+\frac{1}{5^2}+\cdots=\frac{\pi^2}{8}}$
- $\dps{1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{\pi^2}{6}}$
証明 Ex.12 で $x=0$ とおけば
$\dps{\pi=\frac{\pi}{2}+\frac{4}{\pi}\left(1+\frac{1}{3^2}+\frac{1}{5^2}+\cdots\right)}$
となり、(1) が言えます。(2) は、
$\dps{S=1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots}$
とおくと、
\begin{align}
S-\frac{1}{2^2}S
&=\left(1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots\right)
-\left(\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+\cdots\right) \\
&=1+\frac{1}{3^2}+\frac{1}{5^2}+\cdots=\frac{\pi^2}{8} \\
\end{align}
より。
(証明終)

