応用数学 第1回 (6) 同次形に変形するテクニック
同次形に変形するテクニック
Ex.12 $(3x+2y+1)\,dx+(2x-y-4)\,dy=0$。
$1$ や $-4$ が無ければ同次形ですが、このままでは同次形ではありません。そこで
Technique 13 2直線
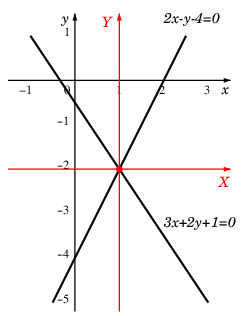
$3x+2y+1=0$, $2x-y-4=0$
の交点 $(a,b)$ を求めて
$X=x-a$, $Y=y-b$
とおけ。
$(a,b)=(1,-2)$, $x=X+1$, $y=Y-2$ であり、
$dx = dX$, $dy = dY$,
$\dps{-\frac{3x+2y+1}{2x-y-4}=-\frac{3(X+1)+2(Y-2)+1}{2(X+1)-(Y-2)-4}=-\frac{3X+2Y}{2X-Y}}$
となって、同次形
$\dps{\frac{dY}{dX}=-\frac{3X+2Y}{2X-Y}
=-\frac{3+2\left(\frac{Y}{X}\right)}{2-\left(\frac{Y}{X}\right)}}$
に変形できました。
$\dps{v=\frac{Y}{X}}$, $\dps{f(v)=-\frac{3+2v}{2-v}}$ として
Th.11 を適用し
$\dps{\frac{dv}{dX}=\frac{1}{X}\left(-\frac{3+2v}{2-v}-v\right)=-\frac{1}{X}\left(\frac{3+4v-v^2}{2-v}\right)}$
$\dps{\int\frac{v-2}{v^2-4v-3}dv=-\int\frac{1}{X}dx}$
$\dps{\frac{1}{2}\log(v^2-4v\require{color}\textcolor{red}{-3})=-\log X+C}$ ... 2022.10.6 13:55 訂正
$X^2(v^2-4v-3)=A$ ( $A=\pm e^{2C}$ )
$\dps{v=\frac{Y}{X}}$ より
$Y^2-4XY-3X^2=A$
さらに $X=x-1$, $Y=y+2$ を入れて整理すれば、一般解は
$y^2-4xy-3x^2+8y-2x=B$ ( $B=A-9$ )
です。
※ 座標を $X$, $Y$ に変換すると、
(分母)$=0$ の方程式も (分子)$=0$ の方程式も $(X,Y)=(0,0)$ を通るので
定数項がなくなるところがミソです。