応用数学 第11回 (2) 公式集
公式集
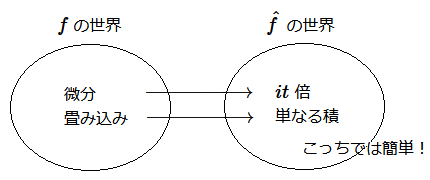
例によって、新しい道具を定義したら公式をたくさん作りましょう。 証明 (1) は積分の線形性より。- $|\,e^{i\theta}\,|=1$ ゆえ、仮定より \begin{align} \widehat{(f')}(t) &=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}f'(x)e^{-itx}dx \\ &=\frac{1}{\sqrt{2\pi}} \left\{\Big[f(x)e^{-itx}\Big]_{-\infty}^{\infty} -(-it)\int_{-\infty}^{\infty}f(x)e^{-itx}dx\right\} \\ &=\frac{1}{\sqrt{2\pi}} \left\{0-0+it\int_{-\infty}^{\infty}f(x)e^{-itx}dx\right\}=it\hat f(t) \\ \end{align}
- $\dps{i(\hat f)'(t) =i\int_{-\infty}^{\infty}\frac{\partial}{\partial t}f(x)e^{-itx}dx =i\int_{-\infty}^{\infty}f(x)(-ix)e^{-itx}dx =\hat g(t)}$
- $\dps{\hat g(t) =\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}f(ax)e^{-itx}dx =\frac{1}{\sqrt{2\pi}} \frac{1}{|\,a\,|}\int_{-\infty}^{\infty}f(u)e^{-i(t/a)u}du =\frac{1}{|\,a\,|}\hat f\left(\frac{t}{a}\right)}$
- $\dps{\hat g(t) =\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}f(x-a)e^{-itx}dx =\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}f(u)e^{-it(u+a)}du =e^{-iat}\hat f(t)}$
畳み込み
証明\begin{align} \sqrt{2\pi}\hat h &=\int_{-\infty}^{\infty} \Big\{ \int_{-\infty}^{\infty}f(x-y)g(y)dy \Big\} e^{-itx}dx \\ &=\int_{-\infty}^{\infty} \Big\{ \int_{-\infty}^{\infty}f(x-y)e^{-itx}dx \Big\} g(y)dy \\ &=\int_{-\infty}^{\infty} \Big\{ e^{-ity}\sqrt{2\pi}\hat f(t) \Big\} g(y)dy \\ &=\sqrt{2\pi}\hat f(t) \int_{-\infty}^{\infty} g(y)e^{-ity}dy = (\sqrt{2\pi})^2\hat f(t) \,\hat g(t) \\ \end{align} (証明終)