応用数学 第10回 (2) 熱伝導方程式の解法
熱伝導方程式
Def.4 次の形の偏微分方程式を「熱伝導方程式」と呼ぶ:
$$c^2\frac{\partial^2 u}{\partial x^2}=\frac{\partial u}{\partial t}
\tag{7.1}
$$
これは、$x$ 軸上に
一様な線密度と一定の比熱
を持つ棒が乗っているときに
$u(x,t)=$ 時刻 $t$ での座標 $x$ での温度
が満たす方程式です。
問 $(7.1)$ を、区間 $0 \leqq x \leqq \ell$ 上で
- 境界条件 $(7.2)$ $u(0,t)=u(\ell,t)=0$
- 初期条件 $(7.3)$ $u(x,0)=f(x)$
のもとで解け ( ただし $f(x)$ は与えられた関数 )。
境界条件は、区間の両端が一定温度であることを、
初期条件の $f(x)$ は時刻 $t=0$ での温度分布を表します。
Step 1 ( 変数分離解 )
まず
$u(x,t)=X(x)T(t)$ ( $X(x)$ は $x$ だけの、$T(t)$ は $t$ だけの関数 )
の形の「変数分離解」を探しましょう。$(7.1)$ へ入れると
$c^2X''T=XT'$
∴ $\dps{\frac{X''}{X}=\frac{1}{c^2}\frac{T'}{T}}$.
左辺は $x$ だけの、右辺は $t$ だけの関数ゆえ
$\dps{\frac{X''}{X}=\frac{1}{c^2}\frac{T'}{T}=}$ 定数 $(-k)$
と置け、
$\dps{
\left\{
\begin{array}{l}
X''+kX=0, \\
T'+c^2kT=0. \\
\end{array}
\right.
}$
$(7.2)$ より
$X(0)=X(\ell)=0$
ですから、
L'a 2 により
$\exists\, n$; $\dps{k=\left(\frac{n\pi}{\ell}\right)^2}$
かつ $\dps{X=A\sin\left(\frac{n\pi x}{\ell}\right)}$.
この $k$ の値を $T'+c^2kT=0$ へ入れて解いて
$\dps{T=B\exp\left(-\left(\frac{n\pi c}{\ell}\right)^2 t\right)}$.
掛け合わせると
$\dps{U = XT = C \sin\left(\frac{n\pi x}{\ell}\right) \exp\left(-\left(\frac{n\pi c}{\ell}\right)^2 t\right)}$.
Step 2 ( 重ね合わせの原理 )
変数分離解を重ね合わせた
$\dps{u(x,t)=\sum_{n=1}^{\infty} C_n \sin\left(\frac{n\pi x}{\ell}\right)
\exp\left(-\left(\frac{n\pi c}{\ell}\right)^2 t\right)}$
も、境界条件 $(7.2)$ を満たす $(7.1)$ の解です。
これが初期条件 $(7.3)$ を満たすように $C_n$ を決めましょう。
$t=0$ を入れると
$\dps{f(x)=u(x,0)
=\sum_{n=1}^{\infty} C_n \sin\left(\frac{n\pi x}{\ell}\right) }$
となり、この式は $f(x)$ のフーリエ正弦展開の係数が $C_n$ であることを示しています。
従って
$\dps{C_n = \frac{2}{\ell}\int_{0}^{\ell}f(x)\sin\left(\frac{n\pi x}{\ell}\right)dx}$.
例
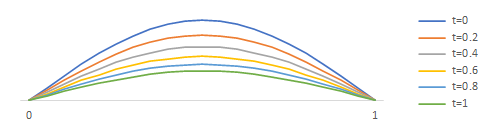
Ex.5 $\ell=1$, $f(x)=\sin(\pi x)$ のとき
$C_1=1$, 他の $C_n=0$ の場合で
$\dps{u(x,t) = \sin(\pi x) \exp\left(-(\pi c)^2 t\right)}$
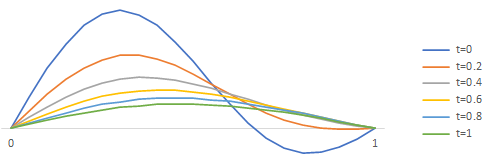
Ex.6 $\ell=1$, $f(x)=\sin(\pi x)+\sin(2\pi x)$ のとき
$C_1=C_2=1$, 他の $C_n=0$ の場合で
$\dps{u(x,t) = \sin(\pi x) \exp\left(-(\pi c)^2 t\right)
+ \sin(2\pi x) \exp\left(-(2\pi c)^2 t\right)}$