応用数学 第9回 (3) 基本定理
フーリエ展開
ここでは $f(x)$ は周期 $2\pi$ を持つ関数とします。
Def.5 $f(x)$ のフーリエ展開とは、次式のように $f(x)$ を三角関数の無限和で表すこと:
$$
f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\Big\{a_n\cos(nx)+b_n\sin(nx)\Big\}
\tag{$\sharp$}
$$
右辺の形を「フーリエ級数」と呼び、
また $a_n$, $b_n$ を「$f(x)$ のフーリエ係数」と呼びます。
Th.6 $f(x)$ も $f'(x)$ も微分可能であれば $f(x)$ はフーリエ展開可能であり、
その係数 $a_n$, $b_n$ は次式で与えられる:
$$
\left\{
\begin{array}{ll}
\dps{a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)dx} & \forall n \geqq 0 \\
\dps{b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)dx} & \forall n \geqq 1 \\
\end{array}
\right.
\tag{$\star$}
$$
$\newcommand{\ip}[2]{\langle\,#1,#2\,\rangle}$
ルーズな証明 $(\sharp)$ が成り立てば
Th.4 より
\begin{align}
\ip{f}{1} &= \ip{\frac{a_0}{2}\times 1}{1}=a_0\pi \\
\ip{f}{\cos(nx)} &= \ip{a_n\cos(nx)}{\cos(nx)}=a_n\pi \\
\ip{f}{\sin(nx)} &= \ip{b_n\sin(nx)}{\sin(nx)}=b_n\pi \\
\end{align}
本当に $=$ になることは難しいので省略します。(証明終)
区分的になめらか
Th.6 が成り立つ条件はもう少し緩められます。
Def.7 $f(x)$ が「区分的になめらか」とは、
- 1周期を有限個の小区間に分けることができて、
- 各小区間の内部では、$f(x)$ は微分可能で、$f'(x)$ も連続関数になり、
- 小区間のつなぎ目でも左右両極限が存在して有限な値である
こと。
ただし
- 左極限とは $\dps{f(x-0)=\lim_{t\, \uparrow\, 0}f(x+t)}$
- 右極限とは $\dps{f(x+0)=\lim_{t\, \downarrow\, 0}f(x+t)}$
です。絵で描くとこんな感じです:
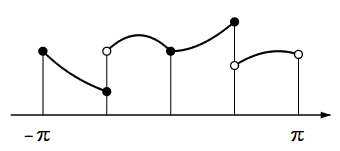
Th.8 $f(x)$ が区分的になめらかであれば
- $f(x)$ の連続点ではフーリエ展開可能であり、$(\sharp)$ が成立する。
- $f(x)$ の不連続点では
$(\sharp)$ の右辺 $\dps{=\frac{1}{2}\Big(f(x-0)+f(x+0)\Big)}$
が成立する。
1ページ目の「ピックで弦を弾いた瞬間」は区分的になめらかですので、
正弦波の無限和で書けることになります。
