応用数学 第1回 (4) 変数分離形微分方程式
変数分離形微分方程式
Def.1 $x$ の関数 $y=y(x)$ について
$$
\frac{dy}{dx}=f(x)g(y)
\tag{2.1}
$$
の形の微分方程式を「変数分離形」と呼ぶ。
ただし、$f(x)$ は $x$ のみの関数、$g(y)$ は $y$ のみの関数とする。
Th.2 $(2.1)$ の一般解は
$\dps{\int\frac{dy}{g(y)}=\int f(x)dx + C}$
証明 $\dps{\frac{1}{g(y)}\frac{dy}{dx}=f(x)}$ の両辺を $x$ で積分すれば、置換積分の公式より。(証明終)
Rem.3 $y$ の方程式
$g(y)=0$
に解 $y=K$ があれば、定数関数 $y(x)=K$ も $(2.1)$ の解になる。
証明 $y(x)=K$ ならば $y'(x)=0$ かつ $f(x)g(y(x))=f(x)g(K)=0$ ゆえ。(証明終)
Ex.4 $\dps{(x-1)\frac{dy}{dx}=2y}$ $\cdots$ $(\ast)$ を解け。
解 これは
$\dps{\frac{dy}{dx}=\left(\frac{2}{x-1}\right)\left(y\right)}$
と書けば $(2.1)$ の形で
$\dps{\int\frac{1}{y}dy=\int\frac{2}{x-1}dx + C}$
$\log|\,y\,|=2\log|\,x-1\,| + C$ $\cdots$ $(\sharp)$
$y=(x-1)^2 \times ( \pm e^C)$
$A=\pm e^C$ とおいて一般解は
$y=A(x-1)^2$
となります。
Rem.5 上の変形では $A\neq 0$ のような気がしますが、
Rem.3 より定数関数 $y(x)=0$ も $(\ast)$ の解ですので $A=0$ でもいいことになります。
という訳で、あまり気にせず $y=A(x-1)^2$ を一般解だと考えましょう。
Rem.6 また、$(\sharp)$ の次を
$2\log|\,x-1\,|=\log|\,y\,| - C$ $\cdots$ $(\sharp)$
$(x-1)^2= y\times ( \pm e^{-C})$
と変形すれば一般解は
$(x-1)^2=By$
であるとも言えます。ここで $B=0$ とおくと $x=1$ という式が得られますが、
直線 $x=1$ 上では $\dps{\frac{dx}{dy}=0}$ $\Rightarrow$ $(x-1)=0=\dps{(2y)\times\frac{dx}{dy}}$
となります。直線 $x=1$ は $y=(x$ の式) の形ではありませんが、
$(\ast)$ を満たす $x$ と $y$ の関係式
であることには違いないので、これも $(\ast)$ の解と考えることにしましょう。
等傾斜法
Rem.6 を更に深読みします。$(\ast)$ を
$\dps{\frac{dy}{dx}=\frac{2y}{x-1}}$
と書けば、この方程式の解は
点 $(x,y)$ で傾き $\dps{\frac{2y}{x-1}}$ をもつような曲線
と考えることができます。実際に点 $(x,y)$ に傾き $\dps{\frac{2y}{x-1}}$ を赤い線でプロットしてみると
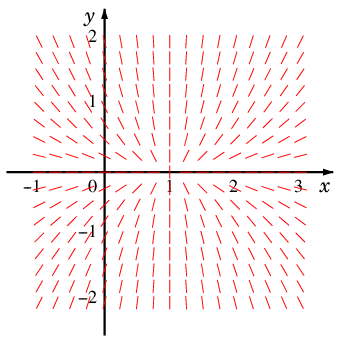
となります。この赤い線をスムーズにつないでできる曲線が $(\ast)$ の解ということになり、
式で書けば、$y = A(x-1)^2$ の形の放物線と、直線 $x=1$ になります。
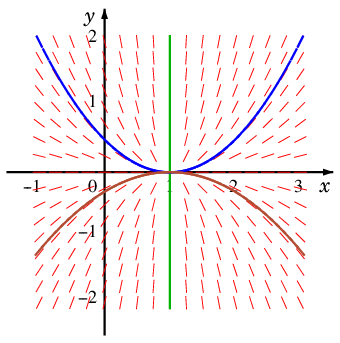
このようにして微分方程式の解を求める方法を「等傾斜法」と言います。



