アルゴリズム論特論(塩田)第13回 (2) 中国剰余定理・中国剰余アルゴリズム
前へ / 戻る / 次へ
$\newcommand{\ol}[1]{\overline{#1}}$
$\newcommand{\znz}[1]{\mathbb{Z}/#1 \mathbb{Z}}$
$\newcommand{\znzc}[1]{(\mathbb{Z}/#1 \mathbb{Z})^{\times}}$
$\newcommand{\inv}[1]{\displaystyle{\frac{1}{#1}}}$
中国剰余定理
Th.1(中国剰余定理、Chinese Remainder Theorem) $m$ と $n$ を互いに素な 2 つの法とするとき、連立合同式
$\dps{
(\ast)\quad
\left\{
\begin{array}{l}
x \equiv a \pmod{m} \\
x \equiv b \pmod{n} \\
\end{array}
\right.}$
は $\bmod (m\times n)$ で唯一の解 $x$ を持つ。
証明 唯一性 $x$, $y$ が共に解であれば
$\dps{
\left\{
\begin{array}{l}
x \equiv a \equiv y \pmod{m} \\
x \equiv b \equiv y \pmod{n} \\
\end{array}
\right.}$
ですから、$x-y$ は $m$ と $n$ の公倍数であり、$\gcd(m,n)=1$ から
$x \equiv y \pmod{(m\times n)}$
存在 は次のアルゴリズムを実行します。
中国剰余アルゴリズム ( CRA )
Algorithm 2(中国剰余アルゴリズム、Chinese Remainder Algorithm) Th.1 の状況で
- 入力:$a$, $b$, $m$, $n$
- 出力:$x$
- $m$, $n$ を引数として拡張ユークリッドアルゴリズムを実行し
$mu+nv=1$
を満たす $u$, $v$ を求める。
- $x = \{\,a(nv)+b(mu)\,\} \,\%\, (m\times n)$ とおく。
証明 1° より
- $\bmod m$ では $1 = mu+nv \equiv nv$, $\ mu \equiv 0$
- $\bmod n\ $ では $1 = mu+nv \equiv mu$, $nv \equiv 0$
となります。わかり易く表にまとめると
| $nu$ | $mu$ |
| $\bmod m$ | $1$ | $0$ |
| $\bmod n$ | $0$ | $1$ |
従って
- $\bmod m$ では $x \equiv a(nv)+b(mu) \equiv a \times 1 + b \times 0 = a$
- $\bmod n\ $ では $x \equiv a(nv)+b(mu) \equiv a \times 0 + b \times 1 = b$
(証明終)
Ex.3 Alg.2 に従って連立合同式
$\dps{
\left\{
\begin{array}{l}
x \equiv 3 \pmod{\ 7\ } \\
x \equiv 5 \pmod{17} \\
\end{array}
\right.}$
を解いてみましょう。
答え
- $7$, $17$ を引数として拡張ユークリッドアルゴリズムを実行し
$7 \times 5 + 17 \times (-1) = 1$
- $x = \{\,3(17 \times (-2))+5(7 \times 5)\,\} \,\%\, (7\times 17)=73$
注
Rem.4
- $(\ast)$ の解のひとつを $x_0$ とおくと、
ふたつの条件式
$x \equiv a \pmod{m}\quad$ かつ $\quad x \equiv b \pmod{n}$
はひとつの条件式
$x \equiv x_0 \pmod{m \times n}$
に書き換えることができる、
ということです。
- $\bmod (m \times n)$ の情報は、
$\bmod m$ の情報と$\bmod n$ の情報の組に分割できる、とも言えます。
- 代数学用語では、
| $\znz{(m \times n)}$ |
$\longrightarrow$ |
$\znz{m}\ \oplus\ \znz{n}$ |
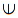 |
|
 |
| $x$ |
$\longmapsto$ |
$(x \,\%\,m,\,x\,\%\,n)$ |
が環の同型になる、と言います。