数値解析 第8回 (3) ホイン法
ホイン法のアイデア
オイラー法では $(9.9)$ の積分を、
区間 $[x_n, x_{n+1}]$ の左端の $x$ 座標を用いて
$f(x,y(x))$ ≒ $f(x_n,y(x_n))$
と考えて、
長方形の面積で近似していました:
$\dps{\int_{x_n}^{x_{n+1}}f(x, y(x))dx}$ ≒ $\dps{h \times f(x_n,y_n)}$
$n=0$ の場合 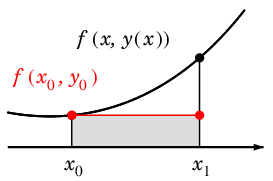
ホイン法ではまず、 $(9.9)$ の積分にある意味「台形公式」を用いて
$\require{color}
\dps{\int_{x_n}^{x_{n+1}}f(x, y(x))dx}$ ≒ $\dps{\frac{h}{2}\Big\{f(x_n,\textcolor{blue}{y(x_n)}) + f(x_{n+1},\textcolor{green}{y(x_{n+1})}\Big\}}$
と考えます。ここでも、$\textcolor{blue}{y(x_n)}$, $\textcolor{green}{y(x_{n+1})}$ の真の値は未知ですから、
- $\textcolor{blue}{y(x_n)}$ には $n$ 番目の近似値 $y_n$ を代入し、
- $\textcolor{green}{y(x_{n+1})}$ には、$n$ 番目の近似値 $y_n$ をオイラー法の近似式に入れて得られる
$\dps{\hat y = y_n + h \times f(x_n,y_n)}$
を代入します。( この $y_n$ はホイン法の近似値です。)
$n=0$ の場合 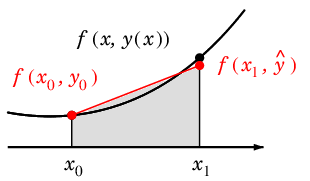
( $\hat y$ は $y(x_1)$ の近似値なので、ふつう $f(x_1,\hat y)$ と $f(x_1,y(x_1))$ は違っています。)
ホイン法の公式
公式 $(9.12)$
$\dps{\hat y = y_n + h \times f(x_n,y_n)}$ として
$\dps{y_{n+1}=y_n + \frac{h}{2} \times \left\{f(x_n,y_n)+f(x_{n+1},\hat y)\right\}}$
$(\,n=0,1,\cdots\,)$
※ ホイン法は、オイラー法を改良した「修正オイラー法」のひとつで、この他にもホイン法と呼ばれる公式がいくつもあります。
実行例
教科書 p.193 図 9.3 では刻み幅 1/1024 で誤差は 0.00052% ほどになり、オイラー法より格段に精度が上がっています。

