数値解析 第7回 (3) ルジャンドル多項式の根
ルジャンドル多項式 $P_n$ の根
ガウスの積分公式では、ルジャンドル多項式の根を用いて観測点を決めます。
その根についての定理です:
Th.9 $P_n$ は区間 $[\,-1,1\,]$ に $n$ 個の異なる実数根を持つ。
更に
- $P_n$ の根を小さい順に $\alpha_1$, $\alpha_2$, $\cdots$, $\alpha_n$
- $P_{n+1}$ の根を小さい順に $\beta_1$, $\beta_2$, $\cdots$, $\beta_{n+1}$
とすると、これらは交互に並んでいる:
$\beta_1 \lt \alpha_1 \lt \beta_2 \lt \alpha_2 \lt \cdots \lt \alpha_n \lt \beta_{n+1}$
絵的に面白いので証明も見ておきましょう。
証明 $n=1$ のときは
$\dps{
\left\{
\begin{array}{l}
P_1=x \\
P_2=\frac{1}{2}(3x^2-1) \\
\end{array}
\right.
}$
ゆえ
$\dps{
\left\{
\begin{array}{l}
\alpha_1=0 \\
\beta_1=-\frac{1}{\sqrt{3}},\quad \beta_2=\frac{1}{\sqrt{3}}\\
\end{array}
\right.
}$
より $\beta_1 \lt \alpha_1 \lt \beta_2$ が成り立ちます。
$n$ のとき正しいと仮定すると、$y=P_n(x)$ のグラフと $\beta_j$ たちの関係は図のようになります:
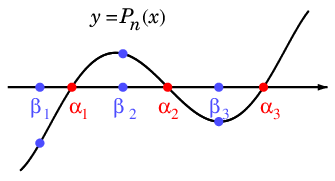
従って
$P_n(\beta_1)$, $P_n(\beta_2)$, $P_n(\beta_3)$, $\cdots$
の符号は毎回逆転します。
Th.3 の漸化式と $P_{n+1}(\beta_j)=0$ から
$\dps{P_{n+2}(\beta_j)=\frac{1}{n+2}\Big\{(2n+3)xP_{n+1}(\beta_j)-(n+1)P_{n}(\beta_j)\Big\}=-\frac{n+1}{n+2}P_{n}(\beta_j)}$
が言えますので
$P_{n+2}(\beta_1)$, $P_{n+2}(\beta_2)$, $P_{n+2}(\beta_3)$, $\cdots$
の符号も毎回逆転し、$y=P_{n+2}(x)$ のグラフは図のようになります。
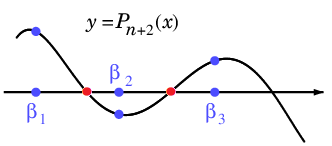
従って区間 $[\,\beta_j,\beta_{j+1}\,]$ ( $j=1,2,\cdots,n$ ) にそれぞれ 1 つ以上 $P_{n+2}$ の根があります。
さらに
Th.4 から $[\,-1,\beta_{1}\,]$ $[\,\beta_{n+1},1\,]$ にも $P_{n+2}$ の根があることがわかります。
(証明終)



