数値解析（塩田）2021年度

数値解析第3回 (2)　二分法

二分法のアイデア

　情報科学では「二分割する作戦」が良く出てきますが、ここでは「解の存在範囲」を二分割します。「存在範囲を二分割する」する作業を繰り返して解を追い詰めていこう、という作戦です。そのキーポイントは

中間値の定理　

$f(x)$ が連続関数で、区間

$[\,a,\ b,]$ の両端で関数値が逆符号

$f(a) \times f(b) \lt 0$ であれば、その区間内に少なくとも１つ

$f(x)=0$ の解

$\alpha$ が存在する。

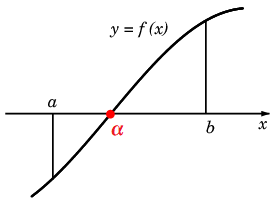
　これをどう使うかと言うと、

二分法のアイデア　さらに

$a$ と

$b$ の中点

$\dps{c=\frac{a+b}{2}}$ を考える。

もし $f(a) \times f(c) \leqq 0$ であれば、区間 $a \lt x \leqq c$ に少なくとも１つ $f(x)=0$ の解が存在し、
そうでなければ区間 $c \lt x \lt b$ に少なくとも１つ $f(x)=0$ の解が存在する。

いずれにしても、解の存在範囲の区間幅を半分に狭めることができる。

二分法のアルゴリズム

Alg.3 ( 二分法 )　

　終了条件としては次のような条件を設定します。

Rem.4　１回のループで区間幅が半分になるということは、２進数として精度が１桁向上することになります。

$2^{20}$ ≒

$10^6$ ですから、ループを 20 回まわせば10進数としての精度が６桁向上します。

Rem.5　２重解はこのままでは求めることができません。解の左右では

$f(x)$ が同符号なので、解の付近で

$f(a) \times f(b) \lt 0$ が成立しないからです。

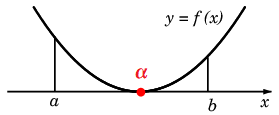
　そこで次の定理を使います。

Th.6　

$\alpha$ が

$f(x)=0$ の２重解であること

$\Leftrightarrow$

$f(\alpha) = f'(\alpha) = 0$ .

　２重解

$\alpha$ は

$f'(x)=0$ の単根ですので、

$f'(x)=0$ について二分法を適用することで

$\alpha$ が求まります。（一般に

$m$ 重解は

$f^{(m-1)}(x)=0$ の単根になります。）