数値解析 第10回 (1) 線形代数の復習
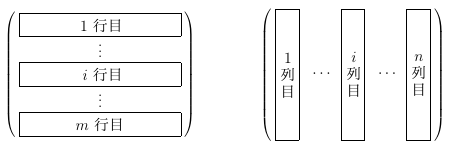
行と列
行列の行と列の区別をちゃんと覚えると、線形代数の理解が随分違います。
- 覚え方: 行の字の中には2本の横棒、列の字の中には2本の縦棒があるので、
横の並びが行、縦の並びが列、と覚えます。

- $(m,n)$-行列、あるいは $m \times n$-行列とは $m$ 個の行と $n$ 個の列を持つ行列のことです。
左の $m$ が行数、右の $n$ が列数です。行、列、の順です。
- $(i,j)$-成分とは $i$ 行目の $j$ 列目の成分のことです。
左の $i$ が行番号、右の $j$ が列番号です。
やはり、行、列、の順です。
- $(i,j)$-成分が $a_{ij}$ である $m \times n$-行列
$A=
\dps{
\mat{ccccccc}{
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\}
}$
を簡単に $A=(a_{ij})$ と表します。
行・列についてもう少し見る
- 行列 $A=(a_{ij})$ と $B=(b_{ij})$ の積 $C=(c_{ij})=AB$ は、
$c_{ij}=$ ( $A$ の第 $i$ 行 ) と ( $B$ の第 $j$ 列 ) の積 $=\dps{\sum_{k}a_{ik}b_{kj}}$
で定義されます。従って積が定義できるのは
( $\ell \times m$-行列 ) と ( $m \times n$-行列 )
のように内側のサイズが揃っている場合です。
-
数ベクトルも行列の一種ですから
( $m$ 次横ベクトル ) と ( $m \times n$-行列 ),
( $m \times n$-行列 ) と ( $n$ 次縦ベクトル )
を掛けることができます。
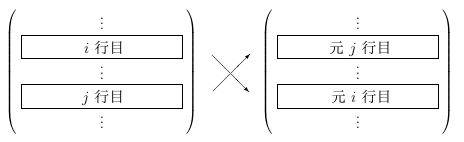
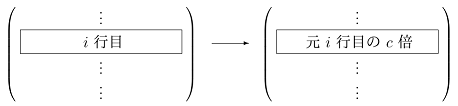
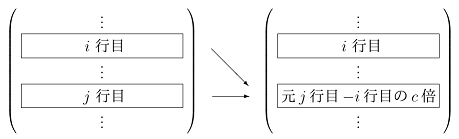
行基本変形
は、今日勉強するガウスの消去法の基本的道具です。
Th.2 行基本変形は可逆な操作である。
すなわち、変形後の行列から、再び行基本変形によって元の行列を得ることができる。
基本行列
次の 3 種類の行列を「基本行列」と言います:
- $m$ 次単位行列の第 $i$ 行と第 $j$ 行を入れ替えた行列 ( $i \neq j$ )
- $(i,i)$-成分が $0$ でないスカラー $c$, 他の成分は単位行列と同じ $m$ 次正方行列
- $(i,j)$-成分がスカラー $-c$, 他の成分は単位行列と同じ $m$ 次正方行列 ( $i \neq j$ )
例えば
(1) $\dps{\mat{rrrr}{0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ }}$
(2) $\dps{\mat{rrrr}{1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ }}$
(3) $\dps{\mat{rrrr}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & -3 & 0 & 1 \\ }}$
のような行列です。
「行基本変形」は「左から基本行列を掛けること」と等しく、
同様に定義される「列基本変形」は「右から基本行列を掛けること」と等しくなります。
これも「左からが行、右からが列」です。
基本行列はその逆行列も基本行列になるので、行・列基本変形は可逆な操作であると言えます。
正則行列
「正則」という形容詞は数学の色んな所で使われますが、行列の正則性についても思い出しておきましょう。
Def.3 $n$ 次正方行列 $A=(a_{ij})$ が次の同値な条件を満たすとき、$A$ を正則行列と言う:
- 逆行列 $A^{-1}$ が存在する
- 行列式 $\det (A)=|\,A\,|$ は $0$ ではない
- $0$ は固有値ではない
- $n$ 次元縦ベクトルの一次変換 $\xxx\mapsto A\xxx$ は一対一写像(全単射)である
- $A$ の階数 $\mbox{rank}(A)$ は $n$ である
- $A$ の $n$ 個の行ベクトルが一次独立である
- $A$ の $n$ 個の列ベクトルが一次独立である
理論背景
- (1) ⇒ (2)
- 行列式は乗法的 ( $|\,AB\,|=|\,A\,|\times|\,B\,|$ ) なので、$A^{-1}$ が存在すれば
$|\,A\,|\times|\,A^{-1}\,|=|\,AA^{-1}\,|=|\,E\,|=1$
となり $|\,A\,|\neq 0$ です。
- (2) ⇒ (1)
- 余因子行列 $\widetilde{A}$ を用いると $A\widetilde{A}=|\,A\,|\,E$ が成り立つので
$|\,A\,|\neq 0$ ならば $A^{-1}=\frac{1}{|\,A\,|}\widetilde{A}$ となります。
- (2) ⇔ (3)
- $|\,A\,|$ は $A$ の全ての固有値の積ゆえ、と言っても良いですし、固有値は固有方程式
$|\,xE-A\,|=0$
の解なので
$0$ が固有値 $\ \Leftrightarrow\ $ $|\,0E-A\,|=0$ $\ \Leftrightarrow\ $ $|\,A\,|=0$
と示してもいいです。
- (1) ⇔ (4)
- $A^{-1}$ が存在すれば $\xxx\mapsto A^{-1}\xxx$ は $\xxx\mapsto A\xxx$ の逆写像になります。
逆に、$\xxx\mapsto A\xxx$ に逆写像が存在すれば、それを表す行列は $A^{-1}$ になります。
- (2) ⇔ (5)
- 行列式を計算する掃き出し法により、
$\mbox{rank}(A) \lt n$ $\ \Leftrightarrow\ $ 行基本変形で成分が全てゼロの行が作れる $\ \Leftrightarrow\ $ $|\,A\,|=0$.
- (5) ⇔ (6) ⇔ (7)
- 階数を計算する掃き出し法により、
$\mbox{rank}(A) \lt n$ $\ \Leftrightarrow\ $ 行基本変形で成分が全てゼロの行が作れる
$\ \Leftrightarrow\ $ 行ベクトルたちが一次従属.
列も同様です。( 転置行列 ${}^tA$ の行列式は $A$ の行列式と等しいので、(6) ⇔ (2) ⇔ (7) という示し方もできます。)