数値解析（塩田）2020年度

数値解析第9回 (4)　偏微分方程式

物理現象を表す偏微分方程式の例

をいくつか見ておきましょう。

ポアソン方程式　 $\dps{\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2 u}{\partial z^2}=f(x, y, z)}$

$u$ は ( 例えば ) 位置 $(x, y, z)$ の静電ポテンシャルを表す関数で、
$f(x,y,z)$ は電荷の分布を表す関数です。

熱伝導方程式　 $\dps{\frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}}$

$u$ は、時刻 $t$, 位置 $(x,y)$ における温度を表す関数です。
拡散方程式とも呼ばれます。

波動方程式　 $\dps{\frac{\partial^2 u}{\partial t^2}=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}}$

$u$ は、時刻 $t$, 位置 $(x,y)$ における波の変位を表す関数です。

ラプラス方程式　 $\dps{\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0,\quad \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2 u}{\partial z^2}=0}$

電荷が存在しない場合の静電ポテンシャルや、熱分布の定常状態などを表します。
ポアソン方程式、熱伝導方程式などの部分問題でもあります。

偏微分方程式の数値解法

　2 変数関数 $u=u(x,y)$ についてのラプラス方程式 $\dps{\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0}$ $\cdots\cdots$ $(1)$ で説明します。

$x$, $y$ の刻み幅 $h = \mathit{\Delta}x = \mathit{\Delta}y$ を設定する。
$xy$-平面に幅 $h$ で格子を描く：
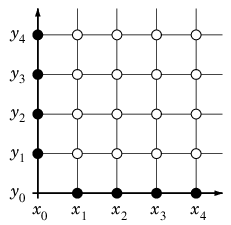
格子点での $u$ の値を $u_{ij}=u(x_i,y_j)$ とおく。
$u_{ij}$ は図の ● では境界条件として与えられていて、○ では未知数である。
$\dps{\frac{\partial^2 u}{\partial x^2}}$ は $y$ を定数と思って $x$ で 2 回微分することなので、中心差分を用いると $\dps{\frac{\partial^2 u}{\partial x^2}(x_i,y_j) \mbox{ ≒ } \frac{1}{h^2}\left(u(x_i+h,y_j)-2u(x_i,y_j)+u(x_i-h,y_j)\right)}$ 4° の記号で $\dps{\frac{\partial^2 u}{\partial x^2}(x_i,y_j) \mbox{ ≒ } \frac{1}{h^2}\left(u_{i+1,j}-2u_{ij}+u_{i-1,j}\right)}$ $\cdots\cdots$ $(2)$ 同様に $\dps{\frac{\partial^2 u}{\partial y^2}(x_i,y_j) \mbox{ ≒ } \frac{1}{h^2}\left(u_{i,j+1}-2u_{ij}+u_{i,j-1}\right)}$ $\cdots\cdots$ $(3)$
$(2)$, $(3)$ を $(1)$ に入れて、≒ を思い切って $=$ と書くと $u_{i+1,j}+u_{i-1,j}+u_{i+1,j}+u_{i-1,j}-4u_{ij}=0$ これを全ての ○ の番号 $(i,j)$ について書き出すと、未知数 $u_{ij}$ たちの連立一次方程式が得られ、それを行列計算によって解く。

　たとえば $10\times 10$ の格子を描くと ○ は 81 個あるので、未知数が 81 個の連立一次方程式を解くことになります。

　ということで、次回から線形代数編に入ります。

前へ / 戻る / 次へ