数値解析 第2回 (3) テイラー展開
そもそもの発想
多項式関数は計算し慣れていて分かり易いですよね。
他の関数 $f(x)$ も、それを近似する多項式関数が分かれば分かり易いのではないかな、
というのがテイラー展開のそもそもの発想です。
1次近似
最初に、関数 $f(x)$ を1次式で近似することを考えましょう。
関数を丸ごと1次式で近似するのは無理なので、
$x=a$ の付近で $f(x)$ を近似する1次式を求めます。
$x=a$ では値が $f(a)$ に一致し、$x=a$ の付近で $f(x)$ に近い直線と言えば
$x=a$ での接線 $\ell$ に他なりません。
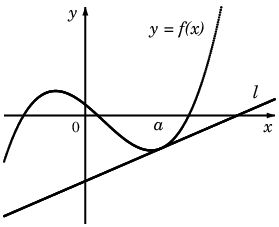
式で書けば
$\ell$ : $y = f'(a)(x-a) + f(a)$
ですから
$x=a$ の付近で $f(x) \mbox{ ≒ } f(a) + f'(a)(x-a)$
という近似式が得られます。$x=a+t$ とおけば、
$t$:十分小で $f(a+t) \mbox{ ≒ } f(a) + f'(a)\,t$
と書くこともできます。ということは
変数 $x$ の値が $a$ から $t$ だけずれると、
$f(x)$ の関数値は $f(a)$ からおおよそ $f'(a)\,t$ だけずれる
という解釈が成り立ちます。$f'(a)\,t$ は「ずれ $t$ の1次式」ですので「1次補正項」と呼ばれます。
2次近似
関数を2次式で近似できれば、「丸み」も表現できて良いのではないか、
というのが次の発想です。結論から書くと
$x=a$ の付近で $\dps{f(x) \mbox{ ≒ } f(a) + f'(a)(x-a) + \frac{1}{2}f''(a)(x-a)^2}$
であり、
$t$:十分小で $\dps{f(a+t) \mbox{ ≒ } f(a) + f'(a)\,t + \frac{1}{2}f''(a)\,t^2}$
です。実際、右辺を $t$ で微分すると
$f'(a) + f''(a)\,t$
となって $f'(x)$ の1次近似式になっていますので、傾き( $=$ 曲がり具合 )も近似できているということです。
$\dps{\frac{1}{2}f''(a)\,t^2}$ が2次補正項になります。
テイラー展開
さらに 3次補正項、4次補正項を考えてゆくと、一般に $n$ 次補正項は
$\dps{\frac{1}{n!}f^{(n)}(a)\,t^n}$
と書けることがわかります( $f^{(n)}$ は $f$ の $n$ 階微分です )。すなわち
$\dps{f(x) \mbox{ ≒ } f(a) + \frac{1}{1!} f'(a)(x-a) + \frac{1}{2!}f''(a)(x-a)^2
+ \frac{1}{3!}f'''(a)(x-a)^3 + \cdots}$
であり、
$\dps{f(a+t) \mbox{ ≒ } f(a) + \frac{1}{1!} f'(a)\,t + \frac{1}{2!}f''(a)\,t^2
+ \frac{1}{3!}f'''(a)\,t^3 + \cdots}$
です。 そして
Th. "良い関数" $f(x)$ に対しては、これらの式は本当に $=$ になる。すなわち
- $x=a$ の付近で
\begin{align}
f(x) &= \sum_{n=0}^{\infty} \frac{1}{n!}f^{(n)}(a)(x-a)^n \\
&= f(a) + \frac{1}{1!} f'(a)(x-a) + \frac{1}{2!}f''(a)(x-a)^2 + \frac{1}{3!}f'''(a)(x-a)^3 + \cdots \\
\end{align}
-
$t$ : 十分小で
\begin{align}
f(a+t) &= \sum_{n=0}^{\infty} \frac{1}{n!}f^{(n)}(a)\,t^n \\
&= f(a) + \frac{1}{1!} f'(a)\,t + \frac{1}{2!}f''(a)\,t^2 \
+ \frac{1}{3!}f'''(a)\,t^3 + \cdots \\
\end{align}
これらを「 $x=a$ における $f(x)$ のテイラー展開」と呼ぶ。
Rem.
$t$ は小さく、$n!$ は巨大な数なので、
$n$ 次補正項 $\dps{\frac{1}{n!}f^{(n)}(a)\,t^n}$ は
$n$ が大きくなれば急速に小さくなる
という感覚を身に付けてください。ここ極めて大事!
マクローリン展開(べき級数展開)
$a=0$ の場合のテイラー展開は特に、「マクローリン展開」あるいは「べき級数展開」とも呼ばれます:
$f(x)$ が "良い関数" ならば、$x=0$ の付近で
$\dps{f(x) = \sum_{n=0}^{\infty} \frac{1}{n!}f^{(n)}(0)\,x^n
= f(0) + \frac{1}{1!} f'(0)\,x + \frac{1}{2!}f''(0)\,x^2 \
+ \frac{1}{3!}f'''(0)\,x^3 + \cdots }$
