フィボナッチ数列

　漸化式 $$ a_{n + 2} = a_{n + 1} + a_n \quad ( n = 0, 1, 2, ... ), \quad a_0 = a_1 = 1 $$ で定められる数列 $\{ a_n \}$ をフィボナッチ数列と呼びます。 始めの数項は $$ 1, \ 1, \ 2, \ 3, \ 5, \ 8, \ 13, \ 21, \ 34, \ 55, \ 89, \ 144, \ 233, \ 377, \ 610, \ 987 $$ で与えられ、自然現象のいろいろな場面に現れる有名な数列です。

　漸化式の特性方程式は $$ X^2 = X + 1 $$ で、特性根 $(1 \pm \sqrt{5})/2$ を用いると一般式は $$ a_n = \frac{1}{\sqrt{5}}\left\{ \left(\frac{1 + \sqrt{5}}{2}\right)^{n + 1} － \left(\frac{1 － \sqrt{5}}{2}\right)^{n + 1} \,\right\} $$ と書くことができます。 （※　大学で線形代数を習った諸君は このページの下 のように一般式を求めましょう。）

黄金比

　$n$ が十分大きければフィボナッチ数列の第 $n$ 項は $$ a_n \mbox{ ≒ } \frac{1}{\sqrt{5}}\left\{ \left(\frac{1 + \sqrt{5}}{2}\right)^{n + 1} \,\right\} $$ となりますので、$n \rightarrow \infty$ のとき隣接２項の比 $( a_{n + 1} / a_n )$ は $( 1 + \sqrt{5} ) / 2$ に収束します。
　$\alpha = ( 1 + \sqrt{5} ) / 2$ は古（いにしえ）より黄金比と呼ばれ、 人間が最も美しいと感じる長方形の縦横比であると言われています。
　黄金比 $\alpha$ の逆数は $1 / \alpha = \alpha － 1$ を満たしますので、これを近似値で書くと $$ 1 / 1.618 ≒ 0.618 $$ また $\alpha^2 = \alpha + 1$ を近似値で書くと $$ 1.618^2 ≒ 2.618 $$ $.618$ は覚えておくと小ネタに使えます。

正五角形の対角線

　一辺の長さが $1$ の正五角形の対角線の長さは黄金比 $\alpha = ( 1 + \sqrt{5} ) / 2$ になります。計算してみましょう。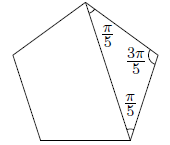 　正五角形の内角は $3\pi /5$ ですから、対角線の長さは $2 \cos(\pi /5)$ と表されます。 $\theta=\pi /5$ とおくと $2\theta= \pi －3\theta$ ですから $$ \sin(2\theta) = \sin(\pi －3\theta) = \sin(3\theta) $$ 倍角、３倍角の公式から $$ 2 \sin(\theta) \cos(\theta) = 3 \sin(\theta) － 4 \sin(\theta)^3 $$ $$ ∴　2 \cos(\theta) = 3 － 4 \sin(\theta)^2 = 3 － 4 ( 1 － \cos(\theta)^2 ) = 4 \cos(\theta)^2 － 1 $$ よって $X = 2 \cos(\pi /5)$ は $X^2 = X + 1$ の正の根、すなわち黄金比になります。

正二十面体の頂点座標

　正多面体は５種類あります。正四面体、立方体、正八面体、正十二面体、正二十面体の５つです。 何か計算しようというときに、頂点座標が上手に与えられていると嬉しいものです。 正四面体の頂点は $$ ( 0, 0, 0 ), \quad ( 0, 1, 1 ), \quad ( 1, 0, 1 ), \quad ( 1, 1, 0 ) $$ が使い易いです。立方体はいいとして、正八面体の頂点は $$ ( \pm 1, 0, 0 ), \quad ( 0, \pm 1, 0 ), \quad ( 0, 0, \pm 1 ) $$ が対称的で綺麗です。正二十面体の頂点は黄金比 $\alpha = ( 1 + \sqrt{5} ) / 2$ を使うと綺麗に書けるそうです： $$ ( 0, \pm 1, \pm\alpha ), \quad ( \pm \alpha, 0, \pm 1 ), \quad ( \pm 1, \pm \alpha, 0 ) $$ ( 参考： Weblog on mebius.tokaichiba.jp 「正20面体の頂点座標の求め方」）

正十二面体の頂点座標

　正四面体の各面の重心を、隣り合う面の重心と結ぶと再び正四面体ができます。 正四面体は自己双対（そうつい）である、と言います。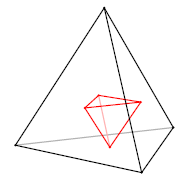 立方体と正八面体はお互いに双対、 正十二面体と正二十面体もお互いに双対です。 正二十面体の頂点座標を元に計算すると、 正十二面体の頂点座標は、黄金比 $\alpha = ( 1 + \sqrt{5} ) / 2$ と、$\beta = ( 2 + \sqrt{5} )$, \quad $\gamma = ( 3 + \sqrt{5} ) / 2$ を用いて $$ ( 0, \pm \beta, \pm \alpha ), \quad ( \pm \alpha, 0, \pm \beta ), \quad ( \pm \beta, \pm \alpha, 0 ), \quad ( \pm \gamma, \pm \gamma, \pm \gamma ) $$ で与えることができます。

ユークリッドの互除法とフィボナッチ数列

　フィボナッチ数列の隣接する２項を、 大きい方からユークリッドの互除法　( division.html 参照 ) の入力にしてみましょう： $$ r_0 = a_n, \quad r_1 = a_{n － 1} $$ すると $r_k = a_{n － k}$ ( $k = 0, 1, 2, \cdots , n$ ) が成り立ちますので $$ \gcd(a_n, a_{n － 1}) = 1 $$ ということも分かりますし、ユークリッドの互除法のループ回数は $n \mbox{ ≒ } \log_\alpha(a_n)$ であることも分かります。
　一般に $a > b > 0$ を満たす２数 $a, b$ を入力したときのユークリッドの互除法のループ回数は $O(\log(a))$ と評価されますが、 フィボナッチ数列の例から、この評価が最良であることがわかります。

加法連鎖

　公開鍵暗号では、べき乗剰余や楕円曲線のスカラー倍などの計算が必要ですが、 このとき「反復２乗法」や「反復２倍法」というアルゴリズムを用いると、 サイド・チャンネル攻撃と呼ばれる攻撃を受ける恐れがあります。 CPU の発する電磁波を測定すると「２乗」や「２倍」のタイミングが読み取れるので、 そこから秘密鍵を読み取れる、という攻撃法です。
　そこで加法連鎖を使うことが提案されました。 加法連鎖とは、数の $1$ から出発して、加法のみを用いて目的の数を作り出す数列のことです。 例えば $11$ を作り出すには \begin{eqnarray*} a_0 &=& 1 \\ a_1 &=& a_0 + a_0 = 1 + 1 = 2 \\ a_2 &=& a_0 + a_1 = 1 + 2 = 3 \\ a_3 &=& a_1 + a_1 = 2 + 2 = 4 \\ a_4 &=& a_2 + a_3 = 3 + 4 = 7 \\ a_5 &=& a_3 + a_4 = 4 + 7 = 11 \\ \end{eqnarray*} のような例があります。 $\{\, 1, \, 2, \, 3, \, 4, \, 7, \, 11 \,\}$ は $11$ を求める長さ $5$ の加法連鎖である、と言います。 これをべき乗剰余 $x^{11} \bmod m$ の計算に使うと、 \begin{eqnarray*} y_0 &=& x \\ y_1 &=& y_0 \times y_0 \bmod m \quad (\ 理論的に = x \times x \bmod m &=& x^2 \bmod m\ ) \\ y_2 &=& y_0 \times y_1 \bmod m \quad (\ 理論的に = x \times x^2 \bmod m &=& x^3 \bmod m\ ) \\ y_3 &=& y_1 \times y_1 \bmod m \quad (\ 理論的に = x^2 \times x^2 \bmod m &=& x^4 \bmod m\ ) \\ y_4 &=& y_2 \times y_3 \bmod m \quad (\ 理論的に = x^3 \times x^4 \bmod m &=& x^7 \bmod m\ ) \\ y_5 &=& y_3 \times y_4 \bmod m \quad (\ 理論的に = x^4 \times x^7 \bmod m &=& x^{11} \bmod m\ ) \\ \end{eqnarray*} のようになり、２乗ではない乗法のみを用いますのでサイド・チャンネル攻撃に耐えられる、という訳です。

　さらに減法も合わせて使うときは加減法連鎖と言います。 楕円曲線では減法と加法は電磁波に差を生じさせずに計算できますので、 スカラー倍計算に加減法連鎖を用いることでサイド・チャンネル攻撃に耐えることができます。 鎖はできるだけ短い方がもちろん計算量が少なくて済みますが、 目的の数を決めて短い鎖を作るのは容易ではありません。 塩田研究室では留学生の Raveen 君が加減法連鎖の研究をしていまして、次のようなアルゴリズムを提案しました。 目的の数 n から逆順に項を計算し、

1. 次の項は、基本的に、黄金比の逆数倍付近の整数にする
2. 数列が黄金比からある程度離れたら、ギャップを小さい数で埋める
3. ギャップを埋めた小さい数たちも連鎖のメンバーに加える

というものです。思わぬところで黄金比が役に立ちました。

黄金比と Hecke 作用素

　保型形式の数値計算をしていると、Hecke 作用素の固有値としてよく黄金比に出会います。 重さ 2, 素数レベルの一変数保型形式の例を少し挙げておきましょう：

• $S_2^{-}(\Gamma_0(23))$ における $T(2)$ の固有値 $0.618034$, $-1.618034$
• $S_2^{-}(\Gamma_0(31))$ における $T(2)$ の固有値 $1.618034$, $-0.618034$
• $S_2^{-}(\Gamma_0(67))$ の2次因子における $T(2)$ の固有値 $0.618034$, $-1.618034$
• $S_2^{+}(\Gamma_0(67))$ における $T(2)$ の固有値 $-0.381966$, $-2.618034$
• $S_2^{+}(\Gamma_0(73))$ における $T(2)$ の固有値 $-0.381966$, $-2.618034$
• $S_2^{+}(\Gamma_0(103))$ における $T(2)$ の固有値 $-0.381966$, $-2.618034$
• $S_2^{+}(\Gamma_0(107))$ における $T(2)$ の固有値 $0.618034$, $-1.618034$
• $S_2^{+}(\Gamma_0(167))$ における $T(2)$ の固有値 $0.618034$, $-1.618034$
• $S_2^{+}(\Gamma_0(191))$ における $T(2)$ の固有値 $0.618034$, $-1.618034$
• $S_2^{+}(\Gamma_0(193))$ の2次因子における $T(2)$ の固有値 $-0.381966$, $-2.618034$
• $S_2^{-}(\Gamma_0(199))$ の2次因子における $T(2)$ の固有値 $0.618034$, $-1.618034$

これは、

• Hecke 作用素の固有値は代数的整数である
• Petersson 予想の結果として、 重さが小さいときは固有値はすべて絶対値が小さい

ことから、２次因子の固有多項式の係数がかなり限定され、$\sqrt{5}$ の体の出動率が高くなる、というのが理由です。

参考：　定数係数線形漸化式

　一般に、隣接 $k + 1$ 項の定数係数線形漸化式 $$ a_{n + k} = c_{k － 1} a_{n + k － 1} + ... + c_1 a_{n + 1} + c_0 a_n\quad (\, n = 0, 1, 2, ...\, ) $$ の解は線形空間を成します。 ( $\{\, a_n \,\}$, $\{\, b_n \,\}$ が共に解であれば、 その一次結合 $\{\, s a_n + t b_n \,\}$ も同じ漸化式を満たす、ということです。) 最初の $k$ 項を決めれば数列が唯一とおりに決まりますので、 解の自由度は $k$、 すなわち、解の成す線形空間の次元は k です。
　特性方程式 $$ X^ k = c_{k－1} X^{k－1} + ... + c_1 X + c_0 $$ の根（特性根）を $\alpha$ とすれば $$ \alpha^{n + k} = c_{k － 1} \alpha^{ n + k － 1} + ... + c_1 \alpha^{n + 1} + c_0 \alpha^n $$ が成り立ちますので $\{\, \alpha^ n \,\}$ はひとつの解を与えます。 さらに $\alpha$ が $m$ 重根であれば $$ { \alpha^ n } , \quad { n \alpha^ n } , ... ,\quad { n^{m － 1} \alpha^ n } $$ たちが全て解になることもわかります。 全ての特性根についてこのような解を書き出せば、 それらが k 個の一次独立な解、すなわち解空間の基底になります。 一般解は基底の一次結合として表され、 初期条件として $a_0, ..., a_{k － 1}$ の値が与えられているときは、 基底の結合係数をそれに合うように決めるだけです。

　フィボナッチ数列の場合、特性方程式 $$ X^2 = X + 1 $$ の２つの解 $$ \alpha = ( 1 + \sqrt{5} ) / 2, \quad \beta = ( 1 － \sqrt{5} ) / 2 $$ は単根ですから、一般解は $$ a_n = A \alpha^ n + B \beta^ n. $$ と書けます。$a_0 = a_1 = 1$ を満たすように $A$, $B$ を求めると $$ A = ( 1 + \sqrt{5} ) / 2 \sqrt{5}, \quad B = ( \sqrt{5} － 1 ) / 2 \sqrt{5} $$ となります。