シンプルな証明

もう見たまんま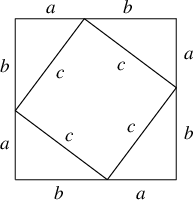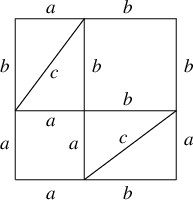： もっともこれは 「 直角三角形 ⇒ $a^2+b^2=c^2$ 」 の証明。 逆向きの 「 $a^2+b^2=c^2$ ⇒ 直角三角形 」も証明してちゃんとしたピタゴラスの定理になります。

ピタゴラス数

　$a^2+b^2=c^2$ を満たす自然数の組 $(a, b, c)$ をピタゴラス数と呼びます。 長いロープがあれば、3, 4, 5 の3辺を持つ三角形は手で作れますから、直角も手で作ることができます。 ピタゴラス数にはそのような効能があります。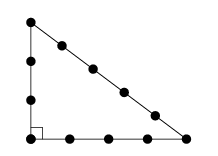

ピタゴラス数の作り方　その１

　素数の性質を使うと、任意のピタゴラス数 $(a, b, c)$ は自然数 $x, y, z$ ( $x > y$ ) を用いて $(a, b, c) = ( (x^2 - y^2)z, 2xyz, (x^2 + y^2)z )\quad$ ( または $a, b$ はその逆 ) と書けることがわかります。$x, y, z$ に好きな数字を入れればいくらでもピタゴラス数を作ることができます。 例えば、

$(x, y, z) = (2, 1, 1) \quad \Rightarrow \quad (a, b, c) = ( 3,  4,  5)$

$(x, y, z) = (3, 2, 1) \quad \Rightarrow \quad (a, b, c) = ( 5, 12, 13)$

$(x, y, z) = (4, 1, 1) \quad \Rightarrow \quad (a, b, c) = (15,  8, 17)$

$(x, y, z) = (4, 3, 1) \quad \Rightarrow \quad (a, b, c) = ( 7, 24, 25)$

$(x, y, z) = (5, 2, 1) \quad \Rightarrow \quad (a, b, c) = (21, 20, 29)$

$(x, y, z) = (5, 4, 1) \quad \Rightarrow \quad (a, b, c) = ( 9, 40, 41)$

といった具合です。（ $x$ と $y$ は互いに素で、偶奇を異にする、という条件をつけても大丈夫です。）

ピタゴラス数の作り方　その２

　ひと組のピタゴラス数 $(a, b, c)$ から、幾何学的に新たなピタゴラス数を作り出すことができます。

　$(x, y) = \displaystyle{\left(\frac{a}{c}, \frac{b}{c}\right)}$ と置くと、$P = (x, y)$ は単位円 $x^2 + y^2 = 1$ の上の点になります。 単位円の外側の$x$軸上に有理数の座標を持つ点 $Q$ を取り、直線 $PQ$ を考えると、 $PQ$ と単位円は $P$ の他のもう一点 $R = (X, Y)$ で交わり、 この $R$ の座標は有理数になります。 $X, Y$ を通分して $\displaystyle{\frac{A}{C}}$, $\displaystyle{\frac{B}{C}}$ とすれば、$(|A|, |B|, C)$ は再びピタゴラス数となります。 　例えば $(a, b, c) = (12, 5, 13)$ のとき、$\displaystyle{P = \left(\frac{12}{13}, \frac{5}{13}\right)}$ です。 $Q = (2, 0)$ を取ると、直線 $PQ$ の方程式は $\displaystyle{y = －\frac{5}{14}(x－2)}$, $\displaystyle{R = \left(－\frac{8}{17}, \frac{15}{17}\right)}$ となって、 新しいピタゴラス数 $(8, 15, 17)$ が得られました。

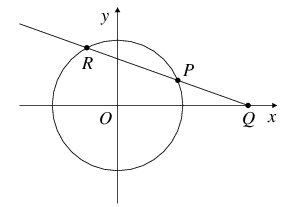
　$PQ$ と単位円がもう一点で交わることは円の方程式が２次式であることから、 $R$ の座標が有理数になることは解と係数の関係からわかります。 この考え方は楕円曲線の加法公式につながってゆきます。

ピタゴラス数の作り方　その３

　単位円 $x^2 + y^2 = 1$ には、 三角関数の加法公式で計算できる群構造があります。 このことを利用すると、２組のピタゴラス数 $(a, b, c)$, $(A, B, C)$ から、第３のピタゴラス数を作り出すことができます。

　上述の通り $\displaystyle{\left(\frac{a}{c}, \frac{b}{c}\right)}$, $\displaystyle{\left(\frac{A}{C}, \frac{B}{C}\right)}$ は単位円 $x^2 + y^2 = 1$ の上の点になりますので、 $$ \left(\frac{a}{c}, \frac{b}{c}\right) = (\cos(\alpha), \sin(\alpha)), \quad \left(\frac{A}{C}, \frac{B}{C}\right) = (\cos(\beta), \sin(\beta)) $$ を満たす $\alpha$, $\beta$ が取れます。すると

$(\cos(\alpha+\beta),\, \sin(\alpha+\beta))$
	$= (\cos(\alpha)\cos(\beta)－\sin(\alpha)\sin(\beta),\, \sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta))$
	$\displaystyle{= \left(\frac{aA-bB}{cC}, \frac{aB+Ab}{cC}\right)}$

は再び単位円上の点となりますので、座標(の絶対値)を通分して再びピタゴラス数が得られます。 例えば $$ (a, b, c) = (3, 4, 5), \quad (A, B, C) = (5, 12, 13) $$ なら、 $$ \left(\frac{aA-bB}{cC}, \frac{aB+Ab}{cC}\right) = \left(－\frac{33}{65}, \frac{56}{65}\right) $$ となってピタゴラス数 $(33, 56, 65)$ が得られました。 （「その１」の方法なら $$ (33, 56, 65) = (7^2－4^2, 2\times 7\times 4, 7^2+4^2) $$ として 得られるものです。）

　同じものを作るのにもいくつもの手段を持っているのは良いことだ、という意味合いでご紹介いたしました。