１次元の無限遠点

　例えば $$ f(x)=\frac{(x^2-5x+6)}{(x-1)^3} $$ という有理式について、どこで $0$ になるか、どこで $\infty$ になるかを考えてみましょう。 分子を因数分解すると $$ f(x)=\frac{(x-2)(x-3)}{(x-1)^3} $$ と書けますから、 $0$ になるのは $x = 2$, $x = 3$ の２箇所、 $\infty$ になるのは $x = 1$ の１箇所 かな、と思いますが、数学者達は長年の経験からこんな数え方を発見しました。

• 分母の $( x － 1 )$ には３乗が付いているので、$x = 1$ では３回 $\infty$ になる、と考える
• $x = \infty$ では、次の式変形から $0$ になると考える：
  $$ f(x)=\left(\frac{1}{x}\right) \frac{\left(1-\left(\dps{\frac{2}{x}}\right)\right)\left(1-\left(\dps{\frac{3}{x}}\right)\right)} {\left(1-\left(\dps{\frac{1}{x}}\right)\right)^3} $$

このように数えると、

• $0$ になるのは $x = 2$, $x = 3$, $x = \infty$ の３箇所で１回ずつ
• $\infty$ になるのは $x = 1$ の１箇所で３回

となり、$0$ になるのも $\infty$ になるのも３回ずつという解釈ができます。

---

　もっと一般的に $$ f(x)= \frac{\left(x\mbox{ の }m\mbox{ 次式}\right)} {\left(x\mbox{ の }n\mbox{ 次式}\right)} $$ の形の有理式でも事情は同じです。 （代数閉体である）複素数体上では $x$ の任意の多項式が一次式に分解しますので、 $f (x)$ の分子 ・ 分母はそれぞれ有限なところで $m$ 回 ・ $n$ 回ずつ 0 になります。 また、 $$ f(x)=\left(\dps{\frac{1}{x}}\right)^{n-m} \frac{\left(\left(\dps{\frac{1}{x}}\right)\mbox{ の }m\mbox{ 次式}\right)} {\left(\left(\dps{\frac{1}{x}}\right)\mbox{ の }n\mbox{ 次式}\right)} $$ という式変形から、$n\mbox{ ≧ }m$ なら、$x = \infty$ では $(n － m)$ 回 $0$ になり、

• $0$ になるのは $m + (n － m) = n$ 回
• $\infty$ になるのは $n$ 回

よって、$0$ になる回数と $\infty$ になる回数は等しくなります。$n ＜ m$ でも同様です。

---

　ここまで曖昧に「 $\infty$ 」と書いてきたものを正確に定義しましょう。

　２つの数の比、の集合（１次元射影空間）を考えます：
$$ \PP^1 = \{\, ( u : v ) \, | \, ( u, v ) \neq ( 0, 0 ) \, \} $$ $v \neq 0$ なら $( u : v ) = ( u/v : 1 )$ ですので、 $\PP^1$ の要素のうち $v \neq 0$ であるものは、写像 $$ u/v \longmapsto x $$ によって数直線（ $x$軸 ）上の点 $x$ と一対一対応します。 $v = 0$ のときは $( u : 0 ) = ( u/u : 0/u ) = ( 1 : 0 )$ ですから、 $v = 0$ となる $\PP^1$ の要素は１つしかありません。 実数体上で絵を描くと $\PP^1$ は円と同じ形をしていて、上記の対応 $u/v \mapsto x$ は下図のように表されます。
$( 1 : 0 )$ だけは $x$軸に投影できないので、これは $x$軸の無限に遠くに投影されると考え、 その投影された点を無限遠点 $\infty$ と呼びます。 右側にある $\infty$ と左側にある $\infty$ は同じ点で、 この点を糊代にして数直線を貼り合わせると円 $= \PP^1$ ができる、というイメージです。

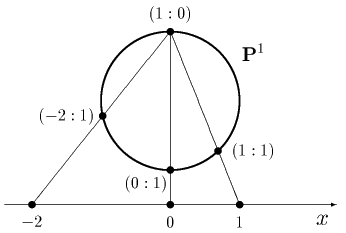
　間違えてはいけないのは、無限遠点は特別な点ではない、ということです。 上の話で $u$ と $v$ を逆にすると、 $u = 0$ となる要素は $( 0 : 1 )$ ひとつ、 $u \neq 0$ である要素は $v/u \mapsto X$ によって数直線（ $X$軸 ）上の点 $X$ と対応する、 ということになります。 $x$軸から見た無限遠点 $( 1 : 0 )$ は $X$軸上の原点 $X = 0$ であり、 $X$軸から見た無限遠点 $( 0 : 1 )$ は $x$軸上の原点 $x = 0$ なのです。

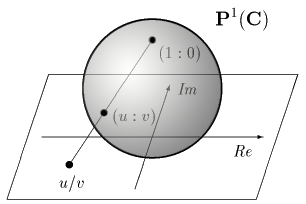
　ちなみに、複素数体上では $\PP^1$ はリーマン球になります。 $( 1 : 0 )$ は北極のようなもので、 $( 1 : 0 )$ 以外の点 $( u : v ) = ( u/v : 1 )$ は複素平面上の点 $u/v$ と図のように一対一対応します。 複素平面の無限遠はどの向きに進んでも $\infty$ という点に辿り着いて、 この $\infty$ を糊代にして複素平面を貼り合わせると球面になる、というイメージです。

２次元の無限遠点

　２次元の無限遠点を定義するには、今度は、３つの数の比の集合（２次元射影空間）を考えます： $$ \PP^2 = \{\, ( u : v : w ) \,|\, ( u, v, w ) \neq ( 0, 0, 0 ) \,\} $$ 　$w \neq 0$ なら $( u : v : w ) = ( u/w : v/w : 1 )$ ですので、 $\PP^2$ の要素のうち $w \neq 0$ であるものは、対応 $$ ( u/w, v/w ) \longmapsto ( x, y ) $$ によって $xy$-平面上の点 $( x, y )$ と対応します。
　$w = 0$ となる要素たちは $( u : v )$ という比で表され、 これは $xy$-平面上の方向ベクトル $(u,v)$ の直線 $v x - u y = 0$ の無限遠に１個ずつあると考えます。 ここでは $\infty_{(u:v)}$ という記号で書くことにしましょう。

２次曲線の分類

　古来、２次曲線は放物線、楕円（円を含む）、双曲線の３種類に分類されてきました。 これらは円錐曲線とも呼ばれ、円錐面を、 母線と平行な平面で切った断面は放物線、 母線より浅い角度を成す平面で切った断面は楕円、 母線より深い角度を成す平面で切った断面は双曲線となります。

　２次元の無限遠点を考えることによってこれらは皆同じものであるという解釈ができます。
　下図のように、放物線 $y = x^2$ は $\infty_{(0:1)}$ で繋がって円になり、
$y = \pm x$ を漸近線にもつ双曲線 $y^2 = x^2 － 1$ は $\infty_{(1:1)}$ と $\infty_{(1:－1)}$ で 繋がってやはり円になる、と考えるのです。

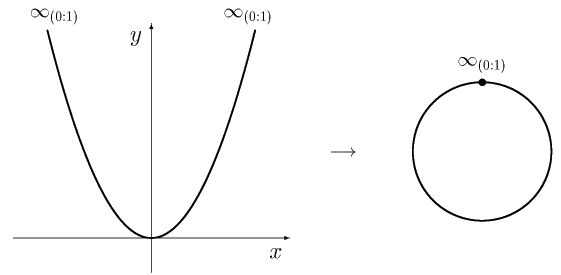
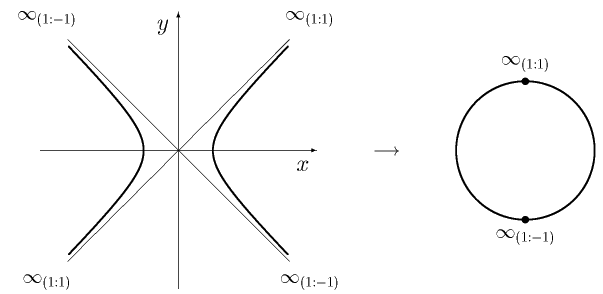
　分類というのは分け方が少ない方がやり易いので、２次曲線は円しかない、 と考えられるという事はとても良い事なのです。

楕円曲線の無限遠点

　楕円曲線 $$ E : y^2 = x^3 + a x + b $$ を $\PP^2 = \{\, ( u : v : w ) \,|\, ( u, v, w ) \neq ( 0, 0, 0 ) \,\}$ の中で考えるには、 $x = u/w$, $y = v/w$ を代入して $$ E : v^2 w = u^3 + a u w^2 + b w^3 $$ と書き換えます。$E$ 上の無限遠点は $w = 0$ を代入するとわかり、$u = 0$、すなわち $( 0 : v : 0 ) = ( 0 : 1 : 0 )$ になります。 前述の通り無限遠点は特別な点ではないのですが、 普通はこれを $O$ と書き表して、加法単位元として採用することが多いです。 理由としては

• $( 0 : 1 : 0 )$ を加法単位元とした加法公式を皆が書き慣れている
• 複素トーラス $\CC / ( \ZZ + \ZZ\tau )$ と楕円曲線 $$ E : y^2 = 4 x^3 - g_2(\tau) x - g_3(\tau) $$ の、ペー関数による一対一対応 $$ \CC / (\ZZ + \ZZ \tau ) \ni z \longmapsto (\wp(z), \wp'(z)) \in E $$ が、複素トーラスの加法単位元 $z = 0$ を $( 0 : 1 : 0 )$ に対応させる

といったことが挙げられるでしょう。

人生は $\pm 0$

　最初の話に戻ります。 代数曲線上の有理関数 $f$ が どこで $0$ になるか、どこで $\infty$ になるかを無限遠点込みで勘定すると、 $0$ になる回数と $\infty$ になる回数が必ず等しくなります。 （正確には、非特異な代数曲線を代数閉体上で考え、有理関数の因子、という言葉で記述します。）

　これは人間にも当てはまることではありませんか。

　人生、山あり谷あり。プラス・マイナス・ゼロ、という言い方もしますし、帳尻が合う、という言い方もあります。 人生は決して良い事だけではありませんが、逆に、悪い事が続いてもいつかは努力が報われる日が来ると信じましょう。

　このように数学は、得てして人生の真実を教えてくれます。