アルゴリズム論特論(塩田) 2020年度教材 第13回
- 出席代わりに、塩田 ( shiota@is.kochi-u.ac.jp ) 宛てにメールを出してください。
- 件名は「アルゴリズム論特論第13回出席」としてください。
$\newcommand{\ol}[1]{\overline{#1}}$
$\newcommand{\znz}[1]{\mathbb{Z}/#1 \mathbb{Z}}$
$\newcommand{\znzc}[1]{(\mathbb{Z}/#1 \mathbb{Z})^{\times}}$
$\newcommand{\inv}[1]{\displaystyle{\frac{1}{#1}}}$
今日のテーマ
拡張ユークリッドアルゴリズムを応用した中国剰余アルゴリズムを今日は勉強します。
暗号の分野では、離散対数問題の解法や、秘密分散法に応用される基本的なアルゴリズムです。
1. 数当てゲーム
まずは次のゲームで遊んでみてください。
セレクトボックスで数字を選んで「答」のボタンを押せば答が表示されます。
数当てゲーム 2桁の自然数をひとつ思い浮かべてください。
その数を当てて見せましょう。
2桁の数字をループで回して条件を満たす数を表示させてるだけじゃないの、
と思かもしれませんが、もっと巨大な数でもできます。
「乱数生成」ボタンで乱数で余りを設定したら「答」ボタンを押してください。
数当てゲーム 128-bit ver. $m_1$, $m_2$, $m_3$ で割った余りから数 $x$ を当てて見せます。
これだって、$x$ を先に作って余りを表示して、それらしく検算を書いてるだけじゃないの、
と思うかもしれませんが、入力欄は自分でも入力できますので、
違う数字を入れてみてください。
($m_i$ を超える数字が入力されたら $m_i$ で割った余りに取り換えます。)
もはや全検索で求められるサイズではありませんが瞬時に答えが出ていますよね。
その仕組みを今日は勉強します。
2. 中国剰余定理・中国剰余アルゴリズム
Th.1(中国剰余定理、Chinese Remainder Theorem) $m$ と $n$ を互いに素な 2 つの法とするとき、連立合同式
$\dps{
\left\{
\begin{array}{l}
x \equiv a \pmod{m} \\
x \equiv b \pmod{n} \\
\end{array}
\right.}$
は $\bmod (m\times n)$ で唯一の解 $x$ を持つ。
証明 唯一性 $x$, $y$ が共に解であれば
$\dps{
\left\{
\begin{array}{l}
x \equiv a \equiv y \pmod{m} \\
x \equiv b \equiv y \pmod{n} \\
\end{array}
\right.}$
ですから、$x-y$ は $m$ と $n$ の公倍数であり、$\gcd(m,n)=1$ から
$x \equiv y \pmod{(m\times n)}$
存在 は次のアルゴリズムを実行します。
Algorithm 2(中国剰余アルゴリズム、Chinese Remainder Algorithm) Th.1 の状況で
- 入力:$a$, $b$, $m$, $n$
- 出力:$x$
- $m$, $n$ を引数として拡張ユークリッドアルゴリズムを実行し
$mu+nv=1$
を満たす $u$, $v$ を求める。
- $x = \{\,a(nv)+b(mu)\,\} \,\%\, (m\times n)$ とおく。
証明 1° より
- $\bmod m$ では $1 = mu+nv \equiv nv$, $\ mu \equiv 0$
- $\bmod n\ $ では $1 = mu+nv \equiv mu$, $nv \equiv 0$
となります。わかり易く表にまとめると
| $nu$ | $mu$ |
| $\bmod m$ | $1$ | $0$ |
| $\bmod n$ | $0$ | $1$ |
従って
- $\bmod m$ では $x \equiv a(nv)+b(mu) \equiv a \times 1 + b \times 0 = a$
- $\bmod n\ $ では $x \equiv a(nv)+b(mu) \equiv a \times 0 + b \times 1 = b$
(証明終)
Ex.3 Alg.2 に従って連立合同式
$\dps{
\left\{
\begin{array}{l}
x \equiv 3 \pmod{\ 7\ } \\
x \equiv 5 \pmod{17} \\
\end{array}
\right.}$
を解いてみましょう。
答え
- $7$, $17$ を引数として拡張ユークリッドアルゴリズムを実行し
$7 \times 5 + 17 \times (-1) = 1$
- $x = \{\,3(17 \times (-2))+5(7 \times 5)\,\} \,\%\, (7\times 17)=73$
Rem.4
- 代数学用語を使って書けば、$m$ と $n$ が互いに素のとき
| $\znz{(m \times n)}$ |
$\longrightarrow$ |
$\znz{m}\ \oplus\ \znz{n}$ |
 |
|
 |
| $x$ |
$\longmapsto$ |
$(x \,\%\,m,\,x\,\%\,n)$ |
が環の同型になる、というのが中国剰余定理です。
- $\bmod (m \times n)$ の情報は、
$\bmod m$ の情報と$\bmod n$ の情報の組に分割できる、とも言えます。
- 暗号で用いるほどのサイズになると
$\bmod (m \times n)$ の計算より$\bmod m$,$\bmod n$ の計算の方が高速に行えますので、
$\!\!\bmod (m \times n)$ の情報が知りたいときに$\bmod m$ と$\bmod n$ で計算しておいて最後に CRA を使う、
という工夫ができます。(ある意味で分割統治法になっています。)
3. 式が 3 個以上のときの中国剰余アルゴリズム
Th.5(中国剰余定理) $m_1$, $\cdots$ $m_k$ を互いに素な $k$ 個の法とするとき、連立合同式
$\dps{
\left\{
\begin{array}{c}
x \equiv a_1 \pmod{m_1} \\
\vdots \\
x \equiv a_k \pmod{m_k} \\
\end{array}
\right.}$
は $\bmod (m_1\times \cdots \times m_k)$ で唯一の解 $x$ を持つ。
証明 唯一性は
Th.1 と同様に示せます。
解は次の
Alg.6 や
Alg.8 で構成できます。
Algorithm 6(中国剰余アルゴリズム) Th.5 の状況で
- 入力:$a_1$, $\cdots$ $a_k$; $m_1$, $\cdots$ $m_k$
- 出力:$x$
$A=a_1$, $M=m_1$
for $i=2$ to $n$ :
新$A =$ 連立合同式 $\dps{
\left\{
\begin{array}{c}
x \equiv A \pmod{M} \\
x \equiv a_i \pmod{m_i} \\
\end{array}
\right.}$ の解
... Alg.2 を用いて求める
新$M = M \times m_i$
$A$ を出力
証明 ループ変数が $i$ のときの 新$A$ は、連立合同式
$\dps{
\left\{
\begin{array}{c}
x \equiv a_1 \pmod{m_1} \\
\vdots \\
x \equiv a_i \pmod{m_i} \\
\end{array}
\right.}$
の解になっていて、この $i$ 個の合同式と
$x \equiv $ 新$A\ ( \bmod$ 新$M)$
が同値になっています。(証明終)
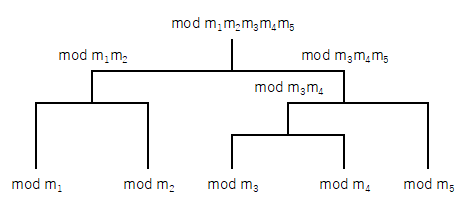
※ 図のようなトーナメントで合同式を制覇してゆくイメージです。
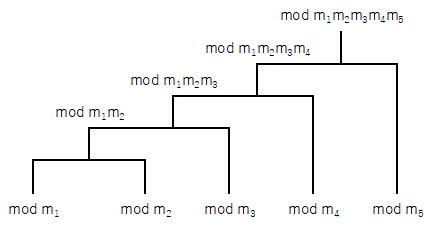
トーナメントはどんな組み方をしても答えは同じになります。
Ex.7 Alg.5 に従って連立合同式
$\dps{
\left\{
\begin{array}{cl}
(1) & x \equiv \ 3\ \pmod{\ 7\ } \\
(2) & x \equiv \ 5\ \pmod{17} \\
(3) & x \equiv 11 \pmod{37} \\
\end{array}
\right.}$
を解いてみましょう。Ex.3 から
(1) かつ (2) $\Leftrightarrow$ $x \equiv 73 \pmod{119}$
でした。ですから
$\dps{
\left\{
\begin{array}{l}
x \equiv 73 \pmod{119} \\
x \equiv 11 \pmod{\ 37\ } \\
\end{array}
\right.}$
を解けばよく
$119 \times 14 + 37 \times (-45) = 1$
から
$x=(73 \times 37 \times (-45) + 11 \times 119 \times 14 ) \,\%\, 4403 = 2453$
次のアルゴリズムは $k$ 個まとめて解くやり方です。
Algorithm 8(中国剰余アルゴリズム) Th.5 の状況で
- 入力:$a_1$, $\cdots$ $a_k$; $m_1$, $\cdots$ $m_k$
- 出力:$x$
- $M=m_1\times \cdots \times m_k$ とおく。
- 各 $i=1,\cdots,k$ に対し、$M_i=M/m_i$ とおく。
- 各 $i=1,\cdots,k$ に対し、$m_i$, $M_i$ を引数として拡張ユークリッドアルゴリズムを実行し
$m_iu_i+M_iv_i=1$
を満たす $u_i$, $v_i$ を求める。
- $\dps{x = \sum_{i=1}^k a_i(M_iv_i) \,\%\, M}$ とおく。
証明 $M_i$ は $m_i$ 以外の法の積なので、
Alg.2 の証明と同様に
| $M_1v_1$ | $M_2v_2$ | $\cdots$ | $M_kv_k$ |
| $\bmod m_1$ | $1$ | $0$ | $\cdots$ | $0$ |
| $\bmod m_2$ | $0$ | $1$ | $\cdots$ | $0$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $\bmod m_k$ | $0$ | $0$ | $\cdots$ | $1$ |
が成り立ちます。従って mod $m_j$ では
$\dps{x \equiv \sum_{i=1}^k a_i(M_iv_i) \equiv a_j(M_jv_j) + \sum_{i \neq j} a_i(M_iv_i)
\equiv a_j\times 1 + \sum_{i \neq j} a_i\times 0 = a_j}$
(証明終)
Ex.9 $m_1=3$, $m_2=5$, $m_3=7$ のとき、
- $M=3\times 5 \times 7=105$
- $M_1=5 \times 7 =35$, $M_2=3 \times 7=21$, $M_3=3 \times 5 =15$
- $3 \times(-23) + 35 \times 2=1$, $5 \times (-4) + 21 \times 1 = 1$, $7 \times (-2) + 15 \times 1 = 1$
- $x = (70 \times a_1 + 21 \times a_2 + 15 \times a_3) \,\%\, 105$
これを使ったのが今日の最初の数当てゲームです。
数字が簡単なので昔から手品に使われていたらしく、
3~5世紀ごろの作と言われる中国の数学書「孫子算経」に書かれていることから中国剰余定理と呼ばれています。
Th.10 Alg.6,Alg.8 の計算量は $O(k\log^2 M)$ である。
特に $k$ が 小さく固定されている場合は $O(\log^2 M)$ になる。
まとめ
- 互いに素な法 $m_1$, $\cdots$ $m_k$ については、「mod $m_1\times\cdots\times m_k$ の情報」は
「mod $m_i$ の情報の組」に読み替えられる。
- その読み替えの計算量は $\log^2$ オーダーである。
自宅学習の例
- デモプログラムでビット数・式の個数を変えて計算量を体感する。
- 違う数字で数当てゲームを作ってみる。
- html の ソースを読んで、Javascript の BigInt の使い方を覚える。
戻る