アルゴリズム論特論（塩田）　2020年度教材第11回

出席代わりに、塩田 ( shiota＠is.kochi-u.ac.jp ) 宛てにメールを出してください。
件名は「アルゴリズム論特論第１１回出席」としてください。 $\newcommand{\ol}[1]{\overline{#1}}$ $\newcommand{\znz}[1]{\mathbb{Z}/#1 \mathbb{Z}}$ $\newcommand{\znzc}[1]{(\mathbb{Z}/#1 \mathbb{Z})^{\times}}$ $\newcommand{\inv}[1]{\displaystyle{\frac{1}{#1}}}$

今日のテーマ

mod $p$ の乗法構造
離散対数問題

　公開鍵暗号の安全性の根拠となる問題は、 RSA 暗号では素因数分解問題でしたが、もう一つ有名なものとして離散対数問題があります。今日はその離散対数とは何者か、というお話です。

1. 観察

　RSA 暗号では、鍵生成や暗号化関数・復号関数で

$x^e \,\%\, n$ という計算（法べき乗）が使われていました。法べき乗は、法が素数のときには特徴的な振る舞いをします。まずはそれを観察してみましょう。

問　

$p$ を素数、

$a$ を法

$p$ の既約剰余類とするとき (

$a \in \znzc{p}$ , 第７回 Def.6 )、

$a^1$ ,

$a^2$ ,

$a^3$ ,

$\cdots$ はどんな振る舞いをするか観察せよ。

例えば $p=7$ , $a=2$ のときは $2^1 = 2$ , $2^2 = 4$ , $2^3 = 1$ , $2^4 = 2$ , $2^5 = 4$ , $2^6 = 1$ となります。 $2^6 = 1$ はフェルマの小定理でわかっていますが、それまでの間は $2$ , $4$ , $1$ , $2$ , $4$ , $1$ という数列になります。
$p=7$ , $a=3$ のときはどうでしょうか。 $3^1 = 3$ , $3^2 = 2$ , $3^3 = 6$ , $3^4 = 4$ , $3^5 = 5$ , $3^6 = 1$ 今度は $3$ , $2$ , $6$ , $4$ , $5$ , $1$ という数列になりました。
$3 \leqq p \leqq 17$ について表を作ってあります。ここから download してしばらく自分で観察してみてください。

観察　こんなことに気付いたでしょうか。

観察　

初めて $a^e = 1$ になる指数 $e$ は $p-1$ の約数である。
一度 $a^e = 1$ になると、その先は繰り返しになる。
その繰り返しの周期は (1) の指数 $e$ に等しい。
$a^1$ , $\cdots$ , $a^{p-1}$ には同じ数が $(p-1)/e$ 回ずつ現れる。
どの素数 $p$ についても、 $a^1$ , $\cdots$ , $a^{p-1}$ がすべて異なるような $a$ が必ずある。
... そのような $a$ だけ赤く塗った表はここから download。

2. mod $p$ の乗法構造

　1. の観察で

$e$ と書いた数はかなり重要な役割を果たしますので名前が付いています。

Def.1　

$p$ を素数、

$a \in \znzc{p}$ とするとき、

$a^e = 1$ となる最小の自然数を「

$a$ の位数 (いすう, order) 」と呼ぶ。

Ex.2　

$p=7$ のとき

$1$ の位数は $1$
$2$ , $4$ の位数は $3$
$3$ , $5$ の位数は $6$
$6$ の位数は $2$

$p=11$ のとき

$1$ の位数は $1$
$2$ , $6$ , $7$ , $8$ の位数は $10$
$3$ , $4$ , $5$ , $9$ の位数は $5$
$10$ の位数は $2$

$p=13$ のとき

$1$ の位数は $1$
$2$ , $6$ , $7$ , $11$ の位数は $12$
$3$ , $9$ の位数は $3$
$4$ , $10$ の位数は $6$
$5$ , $8$ の位数は $4$
$12$ の位数は $2$

　「最小の」というところが効いて次の定理が成り立ちます。

Th.3　

$a \in \znzc{p}$ の位数を

$e$ とするとき、

$a^f=1$ であることと、

$f$ が

$e$ の倍数であることは同値である。

証明　

$\Rightarrow$ )　

$f$ を

$e$ で割って

$f = e q + r$ (

$0 \leqq r \lt e$ ) とおくと

$1 = a^f = (a^e)^q \times a^r = 1^q \times a^r = a^r$ となりますが、

$e$ の最小性から

$r = 0$ . 従って

$f$ は

$e$ の倍数になります。

$\Leftarrow$ )　

$f = e k$ とおけるので

$a^f = (a^e)^k = 1^k = 1$ .(証明終)

　1. の観察結果を定理として書いておきましょう。

Th.4　

$a \in \znzc{p}$ の位数を

$e$ とするとき、次が成り立つ。

$e$ は $p-1$ の約数である。
$a^1$ , $\cdots$ , $a^{p-1}$ は、 $a^e$ から先は繰り返しになる。
(2) の繰り返しの周期は $a$ の位数 $e$ に等しい。
$a^1$ , $\cdots$ , $a^{p-1}$ には同じ数が $(p-1)/e$ 回ずつ現れる。

証明　(1)　フェルマの小定理より

$a^{p-1} = 1$ ですから Th.3 より。

(2)-(4)　これは

$a^{e+1} = a^e \times a^1 = a^1$ ,

$a^{e+2} = a^e \times a^2 = a^2$ ,

$\vdots$ より必然的にそうなります。(証明終)

　観察 (5) も証明されていて

Th.5　任意の素数

$p$ に対して、

$g^1$ ,

$\cdots$ ,

$g^{p-1}$ がすべて異なるような

$g \in \znzc{p}$ が必ず存在する。

　このような

$g$ にも名前がついています。

Def.6　Th.3 の

$g$ を mod

$p$ の生成元 ( generator )、あるいは原始根 ( primitive root ) と呼ぶ。

　さっきまで

$a$ と書いていたのに

$g$ と書いたのは generator の頭文字だからですが、何故 generator と呼ぶかという理由は次の (3) です。

Th.7　次は同値である。

$g$ は mod $p$ の生成元である。
$g^1$ , $\cdots$ , $g^{p-1}$ はすべて異なる
$g^1$ , $\cdots$ , $g^{p-1}$ は全体として $1$ , $2$ , $\cdots$ , $p-1$ に等しい。
$g$ の位数は $p-1$ である。

この状態を群論用語では、「

$\znzc{p}$ は

$g$ によって生成される巡回群である」と言う。

$g$ のべき乗が mod

$p$ のすべての既約剰余類を生成する、と言う意味です。絵としては

$g$ のべき乗たちは巡回的に並んでいるので「巡回群」と呼びます。

$p=7$ ,

$g=3$ の例では次の図のようになって、

$3^6=3^0=1$ から２周目に突入する、という感じです。

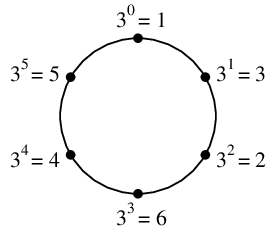Th.7 の証明　

$\znzc{p}$ の要素は丁度

$p-1$ 個あるので (3) が言え、(4) は Th.2 (4) より従います。(証明終)

　Th.5 の証明は初等的にできますが、そんなに短くはないので省略します。（初等整数論あるいは公開鍵暗号の教科書には大抵書いてあります。）

2. 離散対数

　指数関数

$y=a^x$ の逆関数を対数関数と呼ぶことの analogy で、

$y \equiv g^x \pmod{p}$ の逆関数を考えます。

Def.8　

$g$ を mod

$p$ の生成元とするとき、 Th.7 よりすべての

$y \in \znzc{p}$ に対して

$y = g^x$ を満たす指数

$x$ が存在する。この

$x$ を

$x = \log_g y$ と表し「 mod

$p$ における、底

$g$ に対する

$y$ の離散対数」と呼ぶ。

Ex.9　

$p=11$ ,

$g=2$ のとき

$\log_2 3 =$ ？
$\log_2 5 =$ ？
$\log_2 7 =$ ？

$p=13$ ,

$g=2$ のとき

$\log_2 3 =$ ？
$\log_2 5 =$ ？
$\log_2 7 =$ ？

答え

Ex.9　

$p=11$ ,

$g=2$ のとき

$\log_2 3 = 8$
$\log_2 5 = 4$
$\log_2 7 = 7$

$p=13$ ,

$g=2$ のとき

$\log_2 3 = 4$
$\log_2 5 = 9$
$\log_2 7 = 11$

答を折りたたむ

　実数と違って法演算の数には大きさの概念がないので、離散対数の値は全く予測のつかないものとなっています。

　離散対数は

$0 \leqq \log_g y \lt p-1$ の範囲で必ずひとつ見つかりますが、

$g^{p-1}=1$ なので実は自由度があります。

Th.10　

$\log_g\,y$ は mod

$p-1$ で確定する。

証明　

$y = g^x = g^{x'}$ となるための

$x$ ,

$x'$ の必要十分条件は何か、を考える。

$g^x = g^{x'}$	$\Leftrightarrow$	$g^{x-x'}=1$
	$\Leftrightarrow$	$x-x'$ は $g$ の位数の倍数 ( Th.3 )
	$\Leftrightarrow$	$x-x'$ は $p-1$ の倍数 ( Th.7 )
	$\Leftrightarrow$	$x \equiv x' \pmod{(p-1)}$

(証明終) 　この定理により、対数法則は mod 付きで成立することがわかります。

Th.11（対数法則）　

$\log_g(yz) \equiv \log_g y + \log_g z \pmod{(p-1)}$ .

証明　

$y = g^x$ ,

$z = g^{x'}$ とすると

$yz = g^{x+x'}$ ゆえ、Th.10 より

$\log_g(yz) \equiv x + x' \equiv \log_g y + \log_g z \pmod{(p-1)}$ . (証明終)

Ex.12　

$p=13$ ,

$g=2$ ,

$y=5$ ,

$z=7$ のとき、

$\log_g(yz) = \log_2 35 = \log_2 9 = 8$ ,

$\log_g y + \log_g z = \log_2 5 + \log_2 7 = 11 + 9 = 20$ .

$8$ と

$20$ では食い違って見えますが mod

$12$ で一致しています。

Rem.13　実数の対数も、定義域は全ての正数の集合、値域は全ての実数の集合で、定義域と値域は別ものでした。離散対数はそのずれが微妙で、定義域は mod

$p$ , 値域は mod

$p-1$ という訳です。

3. 離散対数問題

Def.14　素数

$p$ , mod

$p$ の生成元

$g$ ,

$y \in \znzc{P}$ を与えたとき

$\log_g\, y$ を求める問題を離散対数問題 ( DLP = Discrete Logarithm Problem ) と呼ぶ。

Th.15　単純検索による mod

$p$ の離散対数問題の計算量は

$O(p\log^2 p)$ .

　計算量に

$p$ が掛かっていますので暗号に使うビット数では天文学的時間がかかります。

証明　

$g^1$ ,

$g^2$ ,

$\cdots$ が

$y$ に一致するまで、

$($

$\times g) \,\%\, p$ という計算を、平均で

$p/2$ 回繰り返さなければならないので。(証明終)

　離散対数問題は一般に困難な問題と考えられていて、このことを利用した暗号技術を次回勉強します。

参考

暗号ライブラリ crypto.py ... 以下のプログラムに引用
単純検索による離散対数計算 DLP.py
... $p$ が 25ビットあたりから実行時間が急激に増えていくはずです。

まとめ

素数を法としたとき、その乗法構造は「巡回群」と呼ばれ、「生成元」と呼ばれる元のべき乗が全ての既約剰余類を生成する。
mod $p$ の既約剰余類 $y$ が生成元 $g$ の何乗になるかを $\log_g y$ と表して「離散対数」と呼ぶ。
mod $p$ の離散対数は mod $p-1$ の数になる。
$p$ , $g$ , $y$ を与えて $\log_g y$ を求める離散対数問題は困難な問題と考えられている。

自宅学習の例

サンプルプログラムを動かしてみる。

戻る