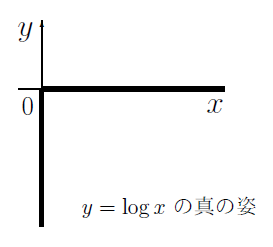アルゴリズム論特論（塩田）　2020年度第1回

はじめに

この授業では公開鍵暗号の理論を題材にして、アルゴリズムとその計算量の理論の勉強をします。
公開鍵暗号では10進数で数百桁の整数を扱いますので、多倍長整数の計算をするプログラミング課題を出します。（ Python や、java の BigInteger 等、多倍長整数の扱える言語を何かひとつ使えるようになりましょう。）
今日は、計算量理論の基礎である、ビット長や、四則演算（加減乗除）の計算量のお話です。
出席代わりに、塩田 ( shiota＠is.kochi-u.ac.jp ) 宛てにメールを頂けると有難いです。教材や授業形態等に関する要望なども遠慮なくお聞かせください。

公開鍵暗号とは

公開鍵暗号では、暗号化に使う鍵（錠前）と復号に用いる鍵（キー）の２種類の鍵を使います。
送信者は、受信者が公開した暗号化鍵を用いて暗号文を作成し、受信者は、自分が秘密に保持している復号鍵を用いて復号を行います。
第三者に解読されないためには、暗号化鍵から復号鍵を計算できないことが必要です。
暗号化関数は一対一写像なので理論的には逆写像が存在するのですが、その計算には天文学的な時間が掛かるので事実上解読されない、という仕組みです。多くの公開鍵暗号では、その仕組みを、整数関数を組み合わせて実現しています。

ビット長

Def.1　正整数（= 自然数）

$n$ の、２進数としての桁数を

$n$ のビット長（またはビット数）と言う。

　次は全て同じことの言い換えです：

$n$ のビット長は $k$ である
$n$ は $k$ -ビットの数である
$n$ は $k$ 桁の２進数として表される

Th.2　自然数

$n$ のビット長を

$k$ とすると

$k = \lfloor \log_2 n\rfloor + 1$ .
（ただし

$\lfloor\ \rfloor$ は切り捨ての記号）

証明　

$k$ -ビットで最小の自然数は

$(100\cdots 00)_2 = 2^{k-1}$ であり、

$k$ -ビットで最大の自然数は

$(111\cdots 11)_2 = 2^k-1$ です。従って

$2^{k-1} \leqq n \leqq 2^k - 1 \lt 2^k.$

$\mbox{∴}\quad k-1 \leqq \log_2 n \lt k.$ つまり

$\log_2 n$ は

$k-1$ 以上

$k$ 未満の実数であるので

$\lfloor \log_2 n \rfloor = k - 1.$ (証明終)

$O$ 記法

Def.3　2つの関数

$f(n)$ ,

$g(n)$ が

$\lim_{n\rightarrow \infty} \left|\frac{f(n)}{g(n)}\right| \leqq \mbox{定数}$ を満たすとき

$f(n) = O(g(n))$ と表す。

これは関数の大きさを大雑把に表す記号です。( 大雑把の $O$ 、といったところです。)
アルゴリズムの計算量を入力引数のビット長で表すために使います。

Ex.4

$100\,n^2 = O(n^2)$ : 定数倍は無視します。
... 入力サイズが2倍になったら計算時間が何倍になるか、といようなうことが知りたくて計算量を測るのですが、そのことには定数倍は必要ないからです。また、マシンスペック（例えばクロック周波数）が違えば同じアルゴリズムでも計算時間は一定の倍数違ってきますので、そこは気にしない、と考えてもよいでしょう。
$n^3+100\,n^2=O(n^3)$ : 多項式関数はべき指数の大きい方が強いので、一番べき指数の大きい項に吸収されます。
$2^n + x^{100} = O(2^n)$ : 指数関数はどんな多項式関数より強力です。逆に言うと、計算量が指数関数であるようなアルゴリズムは使い物にならない、ということです。

Th.5　自然数

$n$ のビット長

$= O(\log n)$

$\log x$ の真の姿

問　関数

$y=\log x$ のグラフは描けますか？

普通の人の答え

　しかし、暗号屋にとってはこういうイメージです：

ここをクリック

　例えば RSA暗号では 2048ビット程度の整数を扱います。

$x=2^{2048}$ 位になると

$\log x = 2048 \times \log 2 \mbox{ ≒ } 1419.565 \lt 2^{11}$ ですから

$\frac{\log x }{x} \lt 2^{11-2048} \lt 2^{-2000} = 1024^{-200} \lt 10^{-600}$ 小数点以下 0 が600個以上続くぐらいグラフは

$x$ 軸にへばりついているわけです。

　計算量にとって

$n$ と

$\log n$ は天と地の差があって、例えば

バブルソートの計算量は $O(n^2)$
マージソートの計算量は $O(n \log n)$

ですから、入力サイズが大きくなればマージソートは遥かにバブルソートより強力、ということになります。

２進数の計算をやってみよう

ここをクリック
とりあえず、足し算と掛け算の問題をやってみてください。

加算器の復習

計算機に２進数の計算をさせるには加算器が必要です。加算器には半加算器 ( half-adder ) と全加算器 ( full-adder ) がありました。 ( 計算機システム論でやりましたね。)
Wikipedia で 加算器の構造 を見てみましょう。

四則演算の計算量

$k$ ビットの２つの整数を足すためには、加算器を $k$ 個並べて、下の桁からの繰上りを順次上の桁用の全加算器に入力していかないといけません。従ってその計算には $k$ に比例した時間が掛かります。つまり $O$ 記法で $O(k)$ の計算量を持つことがわかります。
$k$ ビットの２つの整数の掛け算の計算量は、筆算をイメージして考えましょう。 $k$ ビットの数が $k$ 段並んでいて、それをひとつずつ足すことになるので、その計算時間は　 $k$ $\times$ ( $k$ ビット同士の足し算の計算時間 ) $=O(k^2)$ となります。
２進数の引き算は、２の補数との足し算ですので ( これも計算機システム学でやりましたね )、その計算量は足し算と同じ $O(k)$ です。
割り算は、筆算をイメージすれば掛け算と同様の計算時間が掛かることがわかり、計算量は $O(k^2)$ です。

　以上のことと、先ほどのビット長の定理を合わせると次の定理が得られます：

Th.6　

$n$ 以下の２つの自然数の四則演算の計算量は

加法, 減法は $O(\log n)$
乗法, 除法は $O(\log^2 n)$

$n$

Rem.7　実際には、Python などの多倍長整数ルーティンでは「高速乗算法」が実装されていて、乗法の計算量はもっと低く抑えられています。

　四則演算の計算時間を計測する Python プログラム operations.py で実測できます。（ Python2 で書いてありますので、Python3 の人は適宜書き換えてください。）

まとめ

自然数 $n$ のビット長は $O(\log n)$ .
$n$ 以下の自然数の四則演算の計算量は、加法・減法は $O(\log n)$ , 乗法・除法は $O(\log^2 n)$ .
$\log$ の関数値は極めて小さい。
計算量が $\log$ で書けているアルゴリズムは速い。

自宅学習の例

operations.py を実行して、加減乗除の計算時間を体感してみましょう。

戻る