Processing math: 100%

組合せとグラフの理論（塩田）第13回 (4)　メンガーの定理
前へ / 戻る / 次へ

Menger の定理

　最大フロー・最小カット定理は 「どれだけたくさんデータを送れるか」と「どれだけ小さいカットでブロックできるか」が同じ、 という定理でした。 この現象を重みの無いグラフで考えた Menger の定理を紹介します。まず次の問を考えます。
問　G=(V,E) を連結グラフ、v, w ∈V とするとき、
  1. 辺を共有しない（辺素な、と言います） v-w 道は最大で何本あるか。
  2. 中間点を共有しない（点素な、と言います） v-w 道は最大で何本あるか。
  3. 有向グラフではどうか。
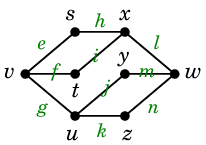
Ex.13　次のグラフで 問 を考えてみましょう。 （黒い記号が頂点、緑の記号が辺です。）
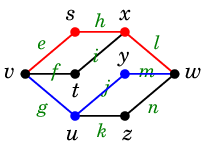
たまたま (1) も (2) も答えは 2 本で、例えば次の図の赤い道と青い道が取れます。
　次はブロックする側の定義です。
Def.14
  1. 辺の部分集合 F⊆E が「vw-非連結化集合」である、とは、任意の v-w 道が F の辺を含むこと。
  2. 頂点の部分集合 W⊆V が「vw-分離集合」である、とは、任意の v-w 道が W の頂点を中間点として含むこと。
言い換えると
  1. ⇔  G−F には v-w 道が無いこと。
  2. ⇔  G−W には v-w 道が無いこと。
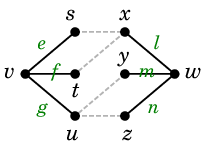
Ex.13 のグラフ
では、例えば {h,i,j,k}, {h,f,g}, {g,ℓ} はいずれも vw-非連結化集合です。
   
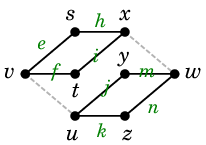G−{h,i,j,k} G−{h,f,g} G−{g,ℓ}

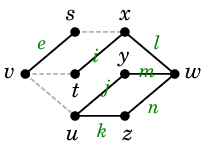
また、{s,t,u} や {u,x} は vw-分離集合です。
 
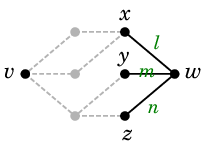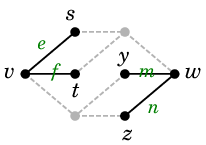G−{s,t,u} G−{u,x}
　この例では、vw-非連結化集合の辺数の最小値も、 vw-分離集合の頂点数の最小値も 2 で 問 の答えに一致していますが、 これが一般にも成り立ちます。
Th.15（辺形の Menger の定理）　辺素な v-w 道の最大数は、vw-非連結化集合の辺数の最小値に等しい。
Th.16（Menger の定理）　点素な v-w 道の最大数は、vw-分離集合の頂点数の最小値に等しい。
Th.17（整数性定理）　Th.15 は有向グラフでも（辺を弧に読み替えて）成り立つ。
証明　Th.17 は全ての弧の容量が 1 の場合の最大フロー・最小カット定理です。 Th.15 は全ての辺 e=xy を 2 本の逆向きの弧 xy, yx に置き換えれば Th.17 に帰着します。 Th.16 も Th.17 の応用として証明されます（Bondy-Murty 11章を参照）。

　今日は最大フロー・最小カット定理から先に証明しましたが、 歴史的には 1927 年にまず Menger が Menger の定理を証明し、 最大フロー・最小カット定理と辺形の Menger の定理は 1956 年に Ford と Fulkerson によって証明されました。

前へ / 戻る / 次へ