Def.1

• 頂点集合 $V$ を 2 つの部分集合 $S$, $\ol{S}$ に分けたとき、 $D$ の弧のうち、 $S$ の頂点から $\ol{S}$ の頂点に至るもの全ての集合を $(S,\ol{S})$ と表す。
• 特に、$S$ が入口 $v$ を含み、$\ol{S}$ が出口 $w$ を含むとき、 この形に書ける弧の集合 $K=(S,\ol{S})$ を「ネットワーク $N$ のカット」と呼ぶ。

Ex.2　次のネットワークではカットは 4 通りあります。

---

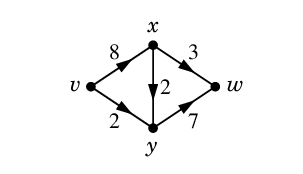
$\require{color}\textcolor{blue}{S_1=\{\,v\,\}}$, $\textcolor{green}{\ol{S_1}=\{\,x,y,w\,\}}$ のとき、 赤い弧たちがカット $\textcolor{red}{K_1=(S_1,\ol{S_1})}$ です。

	→
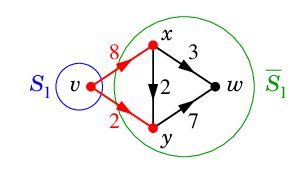
$\textcolor{red}{K_1=(S_1,\ol{S_1})=\{\,vx,vy\,\}}$		$D-K_1$

---

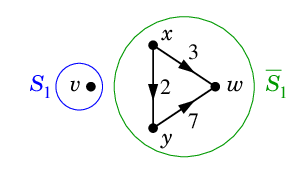
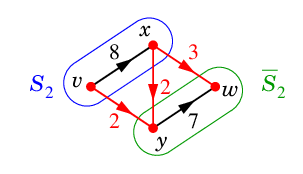
$\textcolor{blue}{S_2=\{\,v,x\,\}}$, $\textcolor{green}{\ol{S_2}=\{\,y,w\,\}}$ のときは

	→
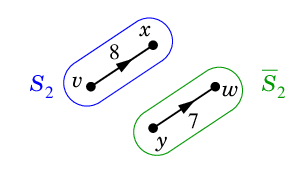$\textcolor{red}{K_2=(S_2,\ol{S_2})=\{\,vy,xy,xw\,\}}$		$D-K_2$

---

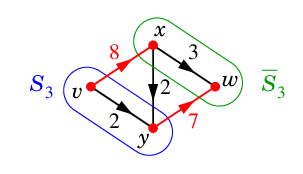
$\textcolor{blue}{S_3=\{\,v,y\,\}}$, $\textcolor{green}{\ol{S_3}=\{\,x,w\,\}}$ のときは $D-K_3$ に弧 $xy$ が残りますが、 向きが $\ol{S_3}$ から $S_3$ へ向かっているのでやはり $v$-$w$ 道はありません。

	→
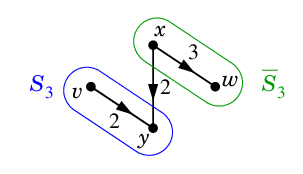$\textcolor{red}{K_3=(S_3,\ol{S_3})=\{\,vx,yw\,\}}$		$D-K_3$

---

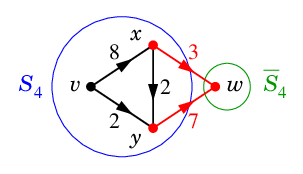
$\textcolor{blue}{S_4=\{\,v,x,y\,\}}$, $\textcolor{green}{\ol{S_4}=\{\,w\,\}}$ のとき

	→
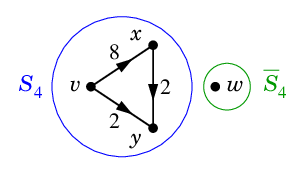$\textcolor{red}{K_4=(S_4,\ol{S_4})=\{\,xw,yw\,\}}$		$D-K_4$

Rem.3 　教科書 p.185 では 「 $D-K$ が $v$-$w$ 道を含まないこと」 を「カット」の定義としていますので、 「Def.1 のカット」は「教科書のカット」のうち極小なもの、 ということになります。

Def.4　

• $D$ 上の重み $f$ と、弧の部分集合 $B$ に対し、 $B$ に属する弧の重みの総和を $\dps{f(B)=\sum_{a \in B} f(a)}$ と表す。
• 特にカット $K=(S,\ol{S})$ に属する弧の容量の総和 $\Psi(K)$ を「カット $K$ の容量」と呼ぶ。
• $N$ のカットの中で容量が最小のものを「$N$ の最小カット」と呼ぶ。