組合せとグラフの理論(塩田)第12回 (2) 定式化
重み付き有向グラフ
(1) の状況をグラフ理論的に表現しましょう。
Def.3
- 重み付き有向グラフは次のように表す。
$N=(D, \Psi)$
- $D=(V,A)$ は有向グラフ
- 弧 $a \in A$ に対して $\Psi(a)$ は $a$ の重みを表す。 ただし $\Psi(a) \geqq 0$ とする。
- 重み付き有向グラフにおいては入出次数は重みの和で定義する:
- $\mbox{indeg}(\Psi,x)=$ $x$ に入る弧 $a$ の重みの和
- $\mbox{outdeg}(\Psi,x)=$ $x$ から出る弧 $a$ の重みの和
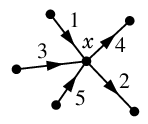 なら
$\left\{
\begin{array}{ll}
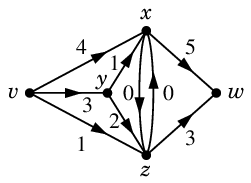
\mbox{indeg}(\Psi,x)\!\!&\!\!=1+3+5=9 \\
\mbox{outdeg}(\Psi,x)\!\!&\!\!=4+2=6 \\
\end{array}
\right.$ です。
なら
$\left\{
\begin{array}{ll}
\mbox{indeg}(\Psi,x)\!\!&\!\!=1+3+5=9 \\
\mbox{outdeg}(\Psi,x)\!\!&\!\!=4+2=6 \\
\end{array}
\right.$ です。
$\Psi$ はギリシャ文字のプサイです。
ネットワーク
Def.4
- 連結な重み付き有向グラフを特に「ネットワーク」と呼ぶ。
- 「ネットワーク」という言葉遣いをするときは、重み $\Psi(a)$ のことを「$a$ の容量」と呼ぶ。
- $\mbox{indeg}(\Psi,x)=0$ となる頂点を「入口」、$\mbox{outdeg}(\Psi,x)=0$ となる頂点を「出口」と呼ぶ。
※ 以下簡単のため、
入口は $v$ 1個、出口は $w$ 1個しかない、とします。
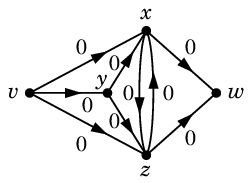
Ex.5(教科書 p.183)
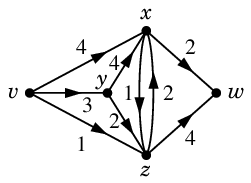
このネットワークでは $v$ が入口、$w$ が出口です。
フロー
次は「流れ」を式で表現しましょう。
Def.6 $D$ 上のもうひとつの重み $\varphi$
(ファイ) が
ネットワーク $N$ の「フロー」であるとは、
- 全ての弧 $a \in A$ について $0 \leqq \varphi(a) \leqq \Psi(a)$ であり、
- 入口 $v$, 出口 $w$ 以外の全ての頂点 $x$ について
$\mbox{indeg}(\varphi,x)=\mbox{outdeg}(\varphi,x)$
が成り立つこと。
それぞれ、前ページの
- 各回線では、回線容量を超えない範囲でデータが送られていること
- 各中継点ではデータの流入量と流出量が釣り合っていること
を表現した式です。
Def.7 フロー $\varphi$ では
入口 $v$ からの流出量 $\mbox{outdeg}(\varphi,v)=$ 出口 $w$ への流入量 $\mbox{indeg}(\varphi,w)$
が成り立つ。この値を「$\varphi$ のフロー値」と呼ぶ。
前ページで、サーバからクライアントへ送られるデータ量 $7$ が「フロー値」です。
Def.8 ネットワーク $N$ を与えたとき、フロー値が最大となるフローを「最大フロー」と呼ぶ。
コンピュータネットワークの場合に役割を整理しておきましょう:
- ネットワークの設定は $N=(D,\Psi)$
- 入口 $v$ はサーバ、出口 $w$ はクライアント
- フロー $\varphi$ はデータが安定して流れている状態
- $\Psi(a)$ は回線 $a$ の容量
- $\varphi(a)$ は回線 $a$ を流れている情報量
- 最大フローは最大通信容量が達成できている状態
- 最大フローの「フロー値」は最大通信容量
「フロー」と「フロー値」をごっちゃにする人がよくいます。間違えないように。
「カレーライス」と「カレーライスの値段」は違うだろ?
ここまでのおさらい
Ex.5 のネットワーク

において、
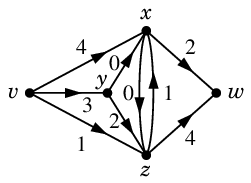
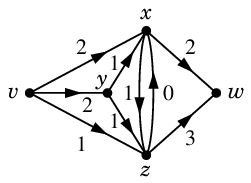
次のうちフローの条件を満たすのはどれ?
答え
フローの条件を満たしているのは (1) と (4) です。
(1) は何も流れていない状態を表し、
ゼロフロー と呼びます。
(2) は $xw$ の重みが容量を超えてしまっています。
(3) は入次数と出次数が中継点の $x$, $y$, $z$ で合っていません。
 なら
$\left\{
\begin{array}{ll}
\mbox{indeg}(\Psi,x)\!\!&\!\!=1+3+5=9 \\
\mbox{outdeg}(\Psi,x)\!\!&\!\!=4+2=6 \\
\end{array}
\right.$ です。
なら
$\left\{
\begin{array}{ll}
\mbox{indeg}(\Psi,x)\!\!&\!\!=1+3+5=9 \\
\mbox{outdeg}(\Psi,x)\!\!&\!\!=4+2=6 \\
\end{array}
\right.$ です。