組合せとグラフの理論(塩田)第8回 (4) 最小連結子問題
最小連結子問題の問題設定
※ コンピュータ間のケーブルの敷設コストが重みであれば、 最小コストでとりあえず通信ができる状態にしよう、ということです。クラスカル法
この問題も決定版のアルゴリズムがあります。実行例
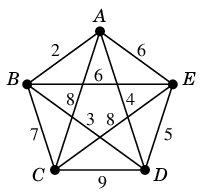
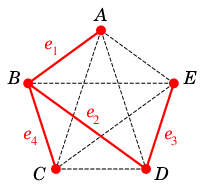
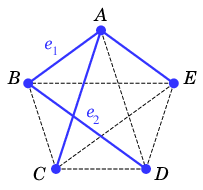
重みの小さい順に辺をソートして考えます。- 重み $2$: $AB=e_1$ を $T$ に付加
- 重み $3$: $BD=e_2$ を $T$ に付加
- 重み $4$: $AD$ は閉路を作るので不採用
- 重み $5$: $ED=e_3$ を $T$ に付加
- 重み $6$: $AE$ は閉路を作るので不採用
- 重み $6$: $BE$ は閉路を作るので不採用
- 重み $7$: $BC=e_4$ を $T$ に付加して終了
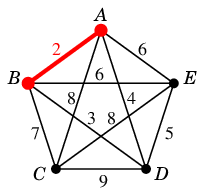 →
(2)
→
(2) 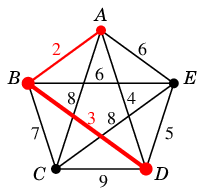 →
→(3)
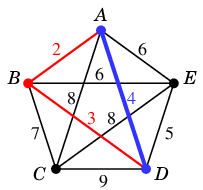 →
(4)
→
(4) 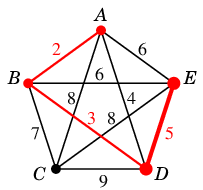 →
→(5)
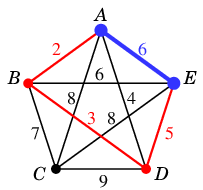 →
(6)
→
(6) 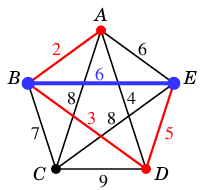 →
→(7)
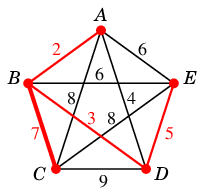 で終了。
で終了。
※ 絵はひとつあれば十分作業できます。
※ これも「ステップ 3° で候補が複数あるときには辞書式順序で一番小さい辺を選ぶ」という追加ルールを設定すれば、誰がやっても同じ結果が得られます。
クラスカル法の証明
$T$ の重み $w(T)$ の最小性を示しましょう。- $S$ を $G$ の任意の全域木
- $e_k$ を、$S$ に含まれない $T$ の辺のうち番号最小のもの
 | $\qquad\qquad$ | 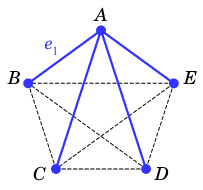 |
| $\require{color}\textcolor{red}{T}$ | $\textcolor{blue}{S}$ |
- $S$ に $e_k$ を付加したグラフ $S_{tmp}$ には閉路 ${\scr C}$ が 1 つだけあります。( 第6回 Th.5 )
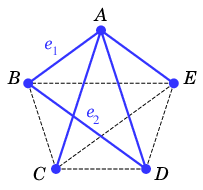
$\qquad\qquad$ 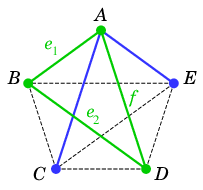
$\textcolor{blue}{S_{tmp}}$ $\textcolor{green}{{\scr C}}$ - $T$ は閉路を含まないので、$T$ に含まれない ${\scr C}$ の辺 $f$ が存在します。
- $S_{tmp}$ から $f$ を除去したグラフを $S'$ とおくと、これは再び $G$ の全域木になります。
$\textcolor{blue}{S'}$ - $S'$ は $e_1$, $e_2$, $\cdots$, $e_k$ を含むことに注意してください。
- Alg.12 3°より $w(e_k) \leqq w(f)$ ですから、
$w(S') = w(S) + w(e_k) - w(f) \leqq w(S)$ - $S$ から $S'$ を作った操作を繰り返すと全ての $e_j$ を含む $T$ ができるので、
$w(T) \leqq \cdots \leqq w(S') \leqq w(S)$