組合せとグラフの理論(塩田)第8回 (1) 重み付きグラフ
重み付きグラフ
今日扱うグラフは全て連結で、かつ、次に定義する「重み付きグラフ」であるとします。
Def.1 全ての辺 $e$ に「重み」と呼ばれる数 $w(e)$ が設定されているグラフを
「重み付きグラフ」と呼ぶ。
Ex.2 重みは辺の横に書き入れます。
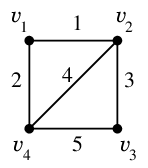
この重み付きグラフは、隣接行列では
$\left(
\begin{array}{cccc}
0 & 1 & 0 & 2 \\
1 & 0 & 3 & 4 \\
0 & 3 & 0 & 5 \\
2 & 4 & 5 & 0 \\
\end{array}
\right)$
のように表します。
(多重辺ありの場合と紛らわしいようですが、
普通、重み付きグラフと多重辺は同時には使いませんので、状況で判断します。)
※ 例えば地図を表すグラフであれば、重みとして
などを設定することができて、
「最短距離でたどり着けるルート」、
「最短時間でたどり着けるルート」、
「一番安い高速料金でたどり着けるルート」
ということが考えられるようになります。