組合せとグラフの理論（塩田）第6回 (3)　幅優先探索
前へ / 戻る / 次へ

幅優先探索のアルゴリズム

　教科書では p.79 で簡単に書いてありますが、大事なアルゴリズムですので時間を掛けてやりましょう。
　「根 ( root )」と呼ばれる頂点を与えて、その根から 幅広く 木を伸ばしてゆき、全域木を作ります。
Algorithm 11（幅優先探索、BFS = Breadth First Search ）
  • 入力：連結なグラフ $G$ と、その頂点 $v$
  • 出力：$v$ を根とする $G$ の幅優先探索木 $T$
  1. $v$ を要素とするキュー $Q=\{\,v\,\}$ を作り、$T$ の初期値は $v$ １点からなる木とする。
  2. $Q$ の先頭から $x$ を取り出す。
  3. 探索点 $x$ の未探索な隣接点のすべてを、番号の小さい順に
    $y_1$, $y_2$, $\cdots$, $y_s$
    とする。
  4. $Q$ の最後尾に $y_1$, $y_2$, $\cdots$, $y_s$ をこの順で追加し、 $T$ には辺 $xy_1$, $xy_2$, $\cdots$, $xy_s$ をすべて付加する。　
  5. $Q$ が空(くう)リストになれば $T$ を出力して終了。そうでなければ 2°へ戻れ。
3°の「未探索な隣接点のすべて」というところが「幅広く」ということです。

例題

$\require{color}$
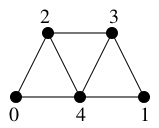
Ex.12　 入力を $G=$ , $v=0$ とします。
  1. $0$ を探索済みとし、 $T=$ 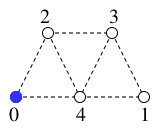, $Q=\{\,\textcolor{blue}{0}\,\}$ .
    ( 青い頂点 は $Q$ の先頭で、次の現在地になります。)
  2. $Q$ の先頭から $\textcolor{blue}{x=0}$ を取り出して現在地とし、$Q=\emptyset$ .
  3. 現在地 $\textcolor{blue}{x=0}$ の未探索な隣接点は $y_1=2$, $y_2=4$ のふたつ。
  4. $y_1=2$, $y_2=4$ を探索済みとして $Q$ の最後尾に追加し $Q=\{\,\textcolor{blue}{2},\,4\,\}$,
    $T$ には辺 $xy_1=02$ と $xy_2=04$ を付加して $T=$ .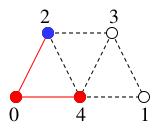
  5. $Q$ の先頭から $\textcolor{blue}{x=2}$ を取り出して現在地とし、$Q=\{\,4\,\}$ .
  6. 現在地 $\textcolor{blue}{x=2}$ の未探索な隣接点は $y_1=3$ .
  7. $y_1=3$ を探索済みとして $Q$ の最後尾に追加し $Q=\{\,\textcolor{blue}{4},\,3\,\}$ ,
    $T$ には辺 $xy_1=23$ を付加して $T=$ .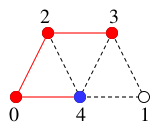
  8. $Q$ の先頭から $\textcolor{blue}{x=4}$ を取り出して現在地とし、$Q=\{\,3\,\}$ .
  9. 現在地 $\textcolor{blue}{x=4}$ の未探索な隣接点は $y_1=1$ .
  10. $y_1=1$ を探索済みとして $Q$ の最後尾に追加し $Q=\{\,\textcolor{blue}{3},\,1\,\}$ ,
    $T$ には辺 $xy_1=41$ を付加して $T=$ .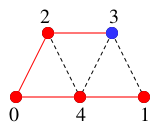
手でやるときは、未探索点が無くなったのでここで終了すればよく、
$T=$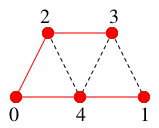
となります。( アルゴリズム的には、このあと $Q$ から $3$, $1$ が取り出されて $Q=\emptyset$ となって終了します。)
手順を表にしてまとめておくと
現在地 $x$$x$ の未探索な隣接点探索木 $T$ に付加する辺キュー $Q$
$\textcolor{white}{,}\textcolor{blue}{0}\textcolor{white}{,}$
$\textcolor{blue}{0}\textcolor{white}{,}$$2$, $4$$02$, $04$$\textcolor{blue}{2}$, $4$
$\textcolor{blue}{2}\textcolor{white}{,}$$3$$23$$\textcolor{blue}{4}$, $3$
$\textcolor{blue}{4}\textcolor{white}{,}$$1$$41$$3$, $1$

Ex.12' 　入力を同じグラフ $G=$ とし、根を $v=1$ とすると、手順は
現在地 $x$$x$ の未探索な隣接点探索木 $T$ に付加する辺キュー $Q$
$\textcolor{white}{,}\textcolor{blue}{1}\textcolor{white}{,}$
$\textcolor{blue}{1}\textcolor{white}{,}$$3$, $4$$13$, $14$$\textcolor{blue}{3}$, $4$
$\textcolor{blue}{3}\textcolor{white}{,}$$2$$32$$\textcolor{blue}{4}$, $2$
$\textcolor{blue}{4}\textcolor{white}{,}$$0$$40$$3$, $0$

となり、幅優先探索木は
$T=$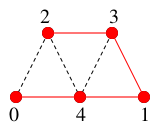
となります。

Ex.12'' 　三たび同じグラフ $G=$ で、根を $v=2$ とした場合、手順は
現在地 $x$$x$ の未探索な隣接点探索木 $T$ に付加する辺キュー $Q$
$\textcolor{white}{,}\textcolor{blue}{2}\textcolor{white}{,}$
$\textcolor{blue}{2}\textcolor{white}{,}$$0$, $3$, $4$$20$, $23$, $24$$\textcolor{blue}{0}$, $3$, $4$
$\textcolor{blue}{0}\textcolor{white}{,}$無し無し$\textcolor{blue}{3}$, $4$
$\textcolor{blue}{3}\textcolor{white}{,}$$1$$31$$4$, $1$

となり、幅優先探索木は
$T=$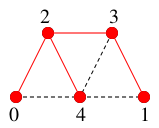
となります。

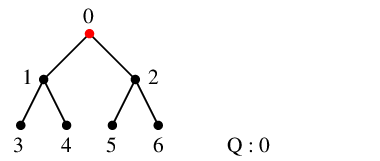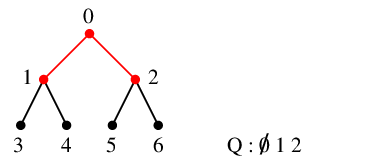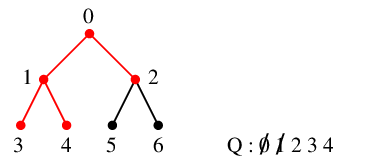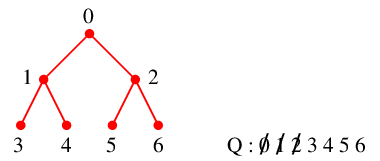
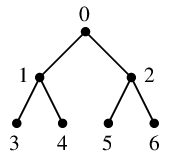
Ex.13 　二分木 $T=$ はそれ自体が全域木ですが、$v=0$ を根とする幅優先探索の手順は

現在地 $x$$x$ の未探索な隣接点探索木に付加する辺キュー $Q$
$\textcolor{white}{,}\textcolor{blue}{0}\textcolor{white}{,}$
$\textcolor{blue}{0}\textcolor{white}{,}$$1$, $2$$01$, $02$$\textcolor{blue}{1}$, $2$
$\textcolor{blue}{1}\textcolor{white}{,}$$3$, $4$$13$, $14$$\textcolor{blue}{2}$, $3$, $4$
$\textcolor{blue}{2}\textcolor{white}{,}$$5$, $6$$25$, $26$$3$, $4$, $5$, $6$

となります。すなわち頂点が探索される順番は $$0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6$$ となります。

Rem.14（ここ大事！） 幅優先探索の要点は
  • 現在地 $x$（青い頂点） からは隣接点までしか見えない
  • 未探索な隣接点のすべてへ枝を伸ばす
ことです。
※　慣れてくれば、キューを横に書くだけで作業できるようになります。

前へ / 戻る / 次へ