組合せとグラフの理論（塩田）2024年度

組合せとグラフの理論（塩田）第3回 (3)　グラフの演算

(1)　和

　単に並べて描くことです。記号は $\cup$ を用います。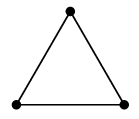

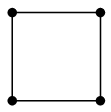
$C_3 \cup C_4$

(2)　頂点の除去

　グラフ $G$ から頂点 $v$ を除去したグラフを $G-v$ と表します。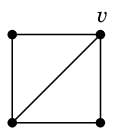

		$\longrightarrow$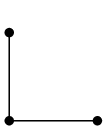
$G$				$G-v$

注意　消した頂点の接続辺も全て消します。こういうのはダメ

(3)　辺の除去

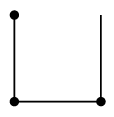
　グラフ $G$ から辺 $e$ を除去したグラフを $G-e$ と表します。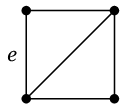

		$\longrightarrow$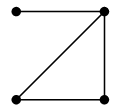
$G$				$G-e$

注意　こちらは、孤立点ができても、それを消してはいけません。

		$\longrightarrow$
$G$				$G-e$

コンピュータネットワークで言えば、$u$ はケーブルを切られて困っているコンピュータ、ということになります。困っている人を切り捨ててはいけない、という感じですね。

(4)　辺の縮約

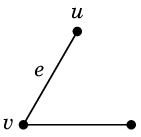
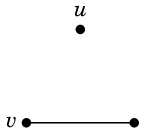
　少し複雑な操作ですが、とても役に立つ演算ですので覚えてください。

　グラフ $G$ から辺 $e=uv$ を縮約したグラフを $G \backslash e$ と表し、次の操作で定義します：

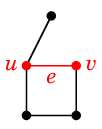		$\longrightarrow$		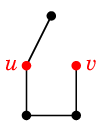		$\longrightarrow$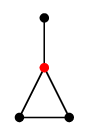
$G$								$G \backslash e$

※　辺 $e=uv$ を 1 点につぶすイメージです。

注意　縮約により多重辺が生じることがありますが、普通はそれを 1 本に減らします。（状況にも依りますが。）

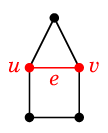		$\longrightarrow$		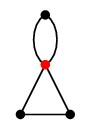		$\longrightarrow$
$G$								$G \backslash e$

(5)　複数の頂点の除去、辺の除去、辺の縮約

　$G-\{\,u,v,w\,\}$, $G-\{\,e,f,g\,\}$, $G\backslash\{\,e,f,g\,\}$ のように表します。また、頂点の部分集合 $W=\{\,u,v,w\,\}$ を用いて $G-W$ というような書き方もします。

Rem.2　除去・縮約は

で活躍します。頂点や辺が減ることで、帰納法の仮定が使えたり、再帰的アルゴリズムが有限の深さで終了する、という仕組みです。詳しくは後日。

(6)　補グラフ

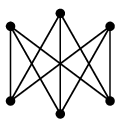
　単純グラフ $G$ に対し、頂点の「隣接する / しない」関係を逆転させたグラフを $G$ の補グラフと呼び、$\overline{G}$ と表します。

		$\longrightarrow$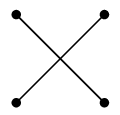
$C_4$				$\overline{C_4}$

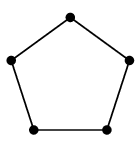
※　$K_4$ から $C_4$ の辺を全て除去したグラフが $\overline{C_4}$ になるイメージです。

Ex.3　$\overline{C_5}$ は $C_5$ と同型になる。（ $C_5$ は自己補対である、と言います。）

これは次のように頂点番号を振るとわかります。

		$\longrightarrow$		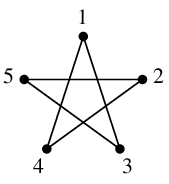		$\cong$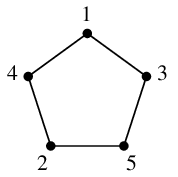
$C_5$				$\overline{C_5}$				$C_5$

Prop.4　補グラフの補グラフ $\overline{\left(\overline{G}\right)}$ は $G$ と同型になる。

証明　隣接関係を２回逆転させるので元へ戻るから。(証明終)

ここ大事！　$\overline{P_n}$ や $\overline{K_{m,n}}$ を描くときは、頂点を一直線に並べない方が良い。

$P_4$ を真っ直ぐ描くと $\overline{P_4}$ の辺が描きにくいですが：

$\longrightarrow$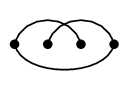

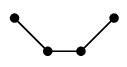$P_4$ の頂点をずらして描いておけばこうなります：

$\longrightarrow$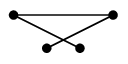

問　$\overline{K_{3,3}}$ を描いてみましょう。