組合せとグラフの理論（塩田）第2回 (3)　頂点の次数
前へ / 戻る / 次へ

頂点の次数

　頂点 $u$ に接続する辺の本数を「 $u$ の次数」と呼び、$\rho(u)$ と表します。（ $\rho$ はギリシャ文字のロー ）
Ex.3　
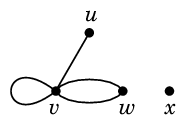
では
  • $\rho(u)=1$ ... 次数 1 の頂点は「端点」と呼びます
  • $\rho(v)=5$ ... ループは 1 本で次数 2 と数えます（理由は後述）
  • $\rho(w)=2$
  • $\rho(x)=0$ ... 次数 0 の頂点は「孤立点」と呼びます
ちょっと脱線　 「弧」は弓へん、「孤立点」の「孤」は子へんで、右側の瓜は「うり」です。 瓜（うり）と爪（つめ）の違いの覚え方は 瓜に爪あり、爪に爪なし です。
赤い部分 が爪で、爪のある方が実は爪ではない、というお話でした。
　ループを 1 本で次数 2 と数える理由は
  • その１ $v$ の近くだけ切り取ると 5 本の辺が出ているように見えるから：
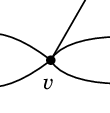
  • その２　次の定理を成り立たせるため：
Th.4（握手補題）　無向グラフ $G=(V,E)$ において、
全ての頂点の次数の和　$\displaystyle{\sum_{v \,\in\, V}\rho(v)=}$ $2$ $\times$ ( $G$ の辺数 ).
従って 次数の和は必ず偶数 になる。
証明　ループでない辺 $e=uv$ は $u$ と $v$ の次数を 1 ずつ増やします。 ループ $e=uu$ は、上述の数え方により、$u$ の次数を 2 増やします。 いずれにしても、辺を 1 本描くごとに次数の和は 2 ずつ増加するので。（証明終）

Cor.5　次数が奇数である頂点は偶数個ある。
　Ex.3 では、辺数は 4 で、次数の和は
$1 + 5 + 2 + 0 = 8 = 2 \times 4$
であり、このうち、奇数は 1 と 5 の 2 個です。

前へ / 戻る / 次へ