戻る / 次へ

グラフの表し方

　もののつながり方に向きを考えないグラフを「無向グラフ」と呼びます。 無向グラフ $G$ は、その頂点集合 $V=V(G)$ と辺集合 $E=E(G)$ のペアとして表します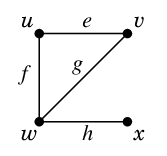： $G=(V,E)$ V は vertex の頭文字、 E は edge の頭文字です。 の場合、$V=\{\,u,v,w,x\,\}$, $E=\{\,e,f,g,h\,\}$ となります。

辺の表し方の工夫

　しかし、 $$V=\{\,u,v,w,x\,\}, \qquad E=\{\,e,f,g,h\,\}$$ という情報を与えられても、絵を見ないとどの頂点がどの辺で結ばれているのかはわかりません。
　そこで、辺 $e$ が頂点 $u$ と $v$ を結ぶ辺であるとき、$e=uv$ と表すことにしましょう： すると上の例では $$V=\{\,u,v,w,x\,\}, \qquad E=\{\,uv, uw, vw, wx\,\}$$ となります。こう書いてあれば絵を復活させることができますね。

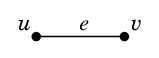
その他の用語

1. ループ
   　ひとつの点から出てその点に戻る辺を「ループ」と呼びます。記号では $e=uu$ のように書ける辺のことです。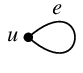
2. 多重辺
   　ふたつの点の間に複数の辺があるとき、それらを「多重辺」と呼びます。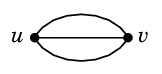
3. 単純グラフ
   　ループも多重辺も持たないグラフを「単純グラフ」と呼びます。
4. 有限グラフ
   　頂点も辺も有限個であるグラフを「有限グラフ」と呼びます。
5. オーダー、サイズ 　漢字は書くのに時間が掛かるので、英語を使って、
   • 頂点数（＝頂点の個数）を「オーダー」
   • 辺数（＝辺の本数）を「サイズ」
   と書くことも多いです。
6. 隣接、接続
   • 頂点と頂点が辺でつながっているとき、また、辺と辺がひとつの頂点を介してつながっているとき、それらは「隣接する」と言います。
   • つながっている頂点と辺は「接続する」と言います。
   　例えば次のグラフでは
   • $u$ の隣接点は $v$ と $w$
   • $u$ と $x$ は隣接しない
   • $e$ と $f$ は隣接する
   • $e$ と $h$ は隣接しない
   • $w$ の接続辺は $f$, $g$, $h$ の３本
   というように使います。
   
   ※　ややこしいようですが、「隣」は同じもの同士に使う言葉、と覚えると良いでしょう。

戻る / 次へ