組合せとグラフの理論(塩田)第10回 (1) 双対グラフ
定義
まずは定義から。
Def.1 平面グラフ $G=(V,E)$ に対し、$\newcommand{\as}{^{\ast}}$
その双対グラフ(幾何学的双対グラフ)$G\as=(V\as, E\as)$ を次のように定める。
- $G\as$ の頂点は $G$ の面のことである。
- $G$ の面 $\alpha$ と $\beta$ が辺を共有するとき、
$G\as$ の頂点として $\alpha$ と $\beta$ を隣接させる。
何のこっちゃ、と思うかもしれませんが、描き方を聴くと意味が分かります。
描き方
描き方
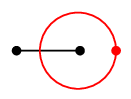
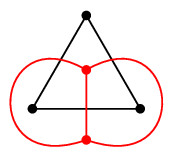
- $G$ の各面に点をひとつずつ打つ
- 隣り合う面に打った点同士を、境界辺をまたぐ辺で結ぶ。
※ $\require{color}\textcolor{red}{G}$
の辺が交差していない ことが前提です。
ここ大事!
Ex.2 正四面体グラフの双対グラフを描いてみましょう(赤いグラフが双対グラフです)。
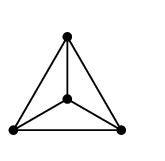 $\displaystyle{\mathop{\longrightarrow}^{\ 1^{\circ}}}$
$\displaystyle{\mathop{\longrightarrow}^{\ 1^{\circ}}}$
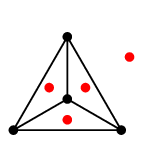 $\displaystyle{\mathop{\longrightarrow}^{\ 2^{\circ}}}$
$\displaystyle{\mathop{\longrightarrow}^{\ 2^{\circ}}}$
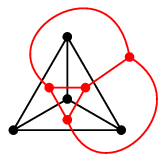 グラフの外側もひとつの面
グラフの外側もひとつの面 ですから忘れないように。
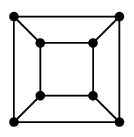
やってみよう Ex.2 をまねて立方体グラフの双対グラフを描いてみましょう。
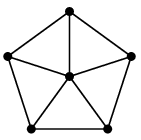
やってみよう 車輪グラフ $W_6$ の双対グラフも描いてみましょう。
注
Rem.3 $G \cong H$ であっても、
平面グラフとしての描画が異なると $G\as \not\cong H\as$ となることがある。(今日の宿題を参照。)
Rem.4 $G$ が単純グラフであっても、$G\as$ にはループや多重辺ができることがある。