組合せとグラフの理論(塩田)第9回 (1) 平面性の定義
平面性の定義
Def.1 平面上に、辺の交差無く描かれているグラフを「平面グラフ」と呼ぶ。
Def.2 平面グラフと同型なグラフを「平面的グラフ」と呼ぶ。
「的」の字があるか無いかはどこが違うのか を、
最初にちゃんと認識しておいてください。
Ex.3 $K_4$ はこう描くと辺が交差していますので平面グラフではありません。
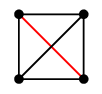
しかし、交差している辺の片方を「外」に出せば、交差を無くすことができます。
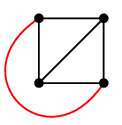
このグラフは平面グラフです。
従ってこの平面グラフと同型な $K_4$ は平面
的グラフ、ということになります。
Ex.4 $K_{2,n}$ も次のように描けば平面的であることがわかります。
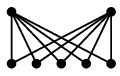 →
→
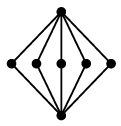
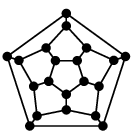
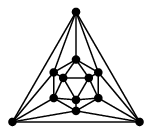
Ex.5 第3回に見たようにプラトングラフは全て平面的です。
 |
|
 |
| 正十二面体グラフ |
|
正二十面体グラフ |
Rem.6
- 「平面グラフか否か」は描画に依存する性質です。
ここ大事!
- これに対し「平面的グラフか否か」は同型で保たれる性質です。
- 「平面的」とは「上手に絵を描けば辺の交差を無くせる」ということです。
Rem.7 電気回路を表すグラフが平面的であれば、
導線を交差させないデザインが可能ですので、
1層の基盤で実現することができ
コストが抑えられます。
とてもいいことです。