組合せとグラフの理論(塩田)第8回 (2) 最短路問題
最短路問題の問題設定
Def.3 重み付きグラフ $G$ 内の歩道や部分グラフに対して、
それが含む辺の重みの合計を、
その歩道や部分グラフの重みと定める。
最短路問題 連結な重み付きグラフ $G$ において、
出発点 $s$ と目的地 $t$ を指定したとき、
重み最小の $s$-$t$ 道を求めよ。
※ 重みが距離の場合がまさしく最短路ですので、それにちなんだネイミングです。
欲張りアルゴリズムは NG
Rem.4 目先の利益しか考えない「欲張りアルゴリズム」では最短路問題は解けない。
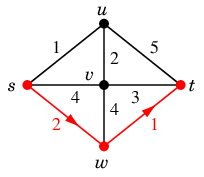
次のグラフで欲張りさんが最短の $s$-$t$ 道を探すとしましょう。
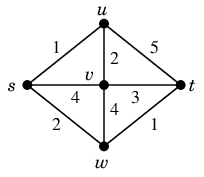
出発点 $s$ から直接見えるのは $u$, $v$, $w$ で、
このうち一番近い $u$ へ進みます。
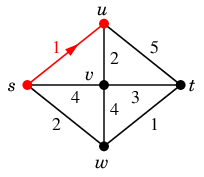
$u$ から直接見えるのは $s$, $v$, $t$ で、
$s$ へ戻っては意味が無いので、
$v$ と $t$ の近い方の $v$ へ進みます。
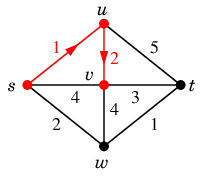
$v$ からは全ての頂点が見えていて、
$s$ や $u$ へは戻らないので、
$w$ と $t$ の近い方の $t$ へ進み、ゴールします。
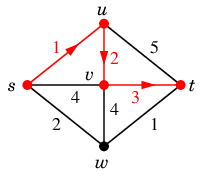
しかし本当の最短路は $s \rightarrow w \rightarrow t$ ですから、
欲張りさんのアルゴリズムでは見つけられません。
ダイクストラ法
最短路問題には決定版のアルゴリズムがあります。
Algorithm 5(ダイクストラ法)
- 入力:連結な重み付きグラフ $G$ と、出発点 $s$、目的地 $t$
- 出力:最短の $s$-$t$ 道
- 全ての頂点 $v$ に仮ラベル $\ell(v)$ を発行する。
- 出発点 $s$ のラベルは $\ell(s)=0$
- $s$ 以外の頂点 $v$ のラベルは $\ell(v)=\infty$
- 親を覚えるためのリストを宣言する。
- 仮ラベルが最小のものをひとつ選び、永久ラベルに昇格させる。
- 目的地 $t$ のラベル $\ell(t)$ が永久ラベルに昇格したら、$t$ から親を辿って最短路を出力し終了する:
$s$ $\rightarrow$ $\cdots$ $\rightarrow$ ($t$ の親の親) $\rightarrow$ ($t$ の親) $\rightarrow$ $t$
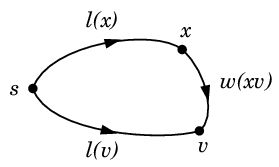
- 今昇格した頂点 $x$ の全ての未昇格な隣接点 $v$ に対し、
$\ell(x)+w(xv) \lt \ell(v)$
であれば
新 $\ell(v)$ $= \ell(x)+w(xv)$, $\quad$ ( $v$ の親 ) $= x$
と更新する。
- 3°に戻る。
永久ラベルは確定した最短距離を表していて、ステップ 5°は、
- $\ell(x)+w(xv)$ $=$ (確定している最短の $s$-$x$ 道 $+$ 辺 $xv$) の距離
- $\ell(v)$ $=$ (今まで見つかっている最短の $s$-$v$ 道の距離)
を比較しています。
Algorithm 5 の追加ルール
ステップ 3° で候補(仮ラベルが最小のもの)が複数あるときは、
親の番号(アスキーコード、アルファベット順 etc.)が一番小さいものを選んで永久ラベルに昇格させる。
更に親が同じ候補が複数あれば、それ自身の番号が一番小さいものを選ぶ。
このルールを追加すると、誰がやっても同じ結果が得られます。
次の例もこの追加ルールありで説明します。
実行例
Ex.6 次のグラフでダイクストラ法(追加ルールあり)を実行し、$A$ から $F$ への最短路を求めてみましょう。
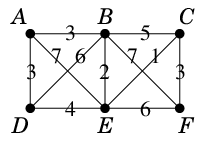
以下、永久ラベルには〇を付け、永久ラベルに昇格したばかりの頂点を青色で示すことにします。
また、最初の仮ラベル $\infty$ は省略し、
親子関係は赤い線で示しています。
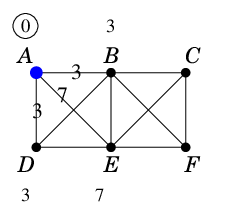 |
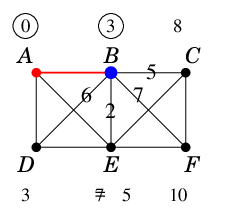
まず出発点の $\ell(A)$ を永久ラベルに昇格させます。
$A$ の隣接点 $B$, $D$, $E$ の仮ラベルを、$A$ からの距離 3, 3, 7 に更新します。 |
 |
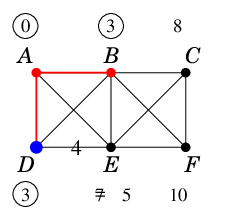
仮ラベル 3 の頂点 $B$, $D$ は親が同じ $A$ ですから、アルファベット順で若い方の $\ell(B)$ を永久ラベルに昇格させます。
$B$ の未昇格な隣接点の仮ラベルを 5°に従って更新します。
特に $E$ は $B$ を経由したルートの方が短いので仮ラベルが 7 から 5 に減ります。 |
 |
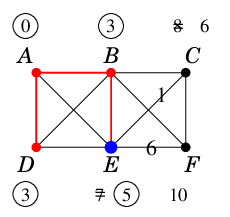
最小の仮ラベル $\ell(D)$ を永久ラベルに昇格させます。
$D$ の未昇格な隣接点は $E$ のみですが、
$D$ を経由しても近くならないので仮ラベルは更新されません。 |
 |
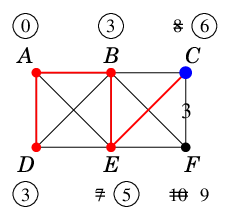
最小の仮ラベル $\ell(E)$ を永久ラベルに昇格させます。
$C$ は $E$ を経由したルートの方が短いので仮ラベルが 8 から 6 に減ります。 |
 |
最小の仮ラベル $\ell(C)$ を永久ラベルに昇格させます。
$F$ は $C$ を経由したルートの方が短いので仮ラベルが 10 から 9 に減ります。 |
 |
目的地のラベル $\ell(F)$ が永久ラベルに昇格して終了します。
最短路は $A$ $\rightarrow$ $B$ $\rightarrow$ $E$ $\rightarrow$ $C$ $\rightarrow$ $F$ となりました。 |
※ 慣れてくれば、グラフの絵ひとつにラベルを書くだけで作業できるようになります。
Prop.7 全ての辺の重みが 1 のときは、
ダイクストラ法(追加ルールあり)を全ての頂点への最短路が求まるまで続けることは、
$s$ を根とする幅優先探索を行うことに等しい。
「永久ラベルに昇格した頂点」が幅優先探索の現在地に当たり、
$\ell(v)$ が $\infty$ から更新された瞬間に $v$ はキューに登録されます。












