組合せとグラフの理論(塩田)第6回 (1) 木
定義と例
まずは木の定義から。 言い換えれば、林とは木の和である、ということになります。 この 3 つのグラフの和をとってひとつのグラフと思うと林になります。木であることの言い換え
木は重要な構造ですので、木である条件をいろいろ言い換えておきましょう。その証明のために補題を用意します: 証明の要点 (1) $e=uv$ を含む閉路が無ければ、 $G$ では同じ連結成分に属していた $u$ と $v$ が、 $G-e$ では異なる連結成分に属します。
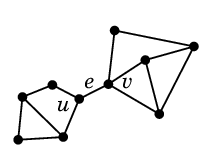
| $\Rightarrow$ |
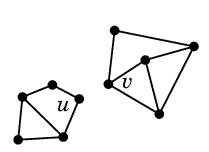
|
| $G$ | $G-e$ |
逆に $e=uv$ を含む閉路が有れば、$G-e$ においても $u$ と $v$ は同じ連結成分に属します。
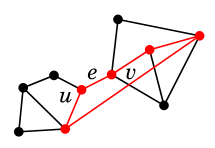
| $\Rightarrow$ |
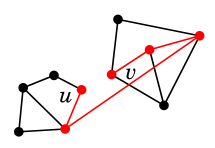
|
| $G$ | $G-e$ |
(2) たとえば次のグラフのように
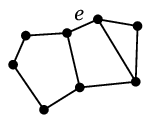
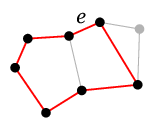 $\phantom{\longrightarrow}$
$\phantom{\longrightarrow}$
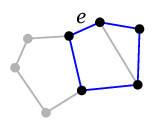
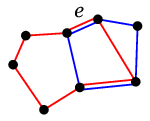 $\longrightarrow$
$\longrightarrow$
Th.5 の証明 (1) ⇒ (2) 辺 $e$ をひとつ取ります。 L'a 6 より $e$ は橋で、 $T-e$ は閉路を含まないので 2 つの木 $T_1$, $T_2$ の和になります。 すると帰納法の仮定から
$=$ ( $T_1$ の頂点数 $-1$ ) $+$ ( $T_2$ の頂点数 $-1$ ) $+1$ $=n-1$
(2) ⇒ (3) $T$ は閉路を持たないので林、すなわち木の和です。 その木の本数を $k$ 本とすれば、(1) ⇒ (2) は既に証明しましたので
教科書にはこの後 (3) ⇒ (4) ⇒ (5) ⇒ (6) ⇒ (1) の証明が書いてあります。 読んでおいてください。(証明以下省略)
 を継ぎ足してゆく
を継ぎ足してゆく