組合せとグラフの理論（塩田）2023年度

組合せとグラフの理論（塩田）第2回 (2)　有向グラフ

有向グラフ

　もののつながり方に向きを考えたグラフを「有向グラフ」( digraph ) と呼びます。有向グラフでは辺とは呼ばず「弧」( arc ) と呼び、頂点 $u$ から出て $v$ へ至る弧を $a=uv$ と表します。

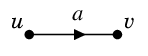
有向グラフ $D$ も、その頂点集合 $V=V(D)$ と弧集合 $A=A(D)$ のペアとして表します： $D=(V,A)$

注意　無向グラフでは $uv$ と $vu$ は同じ辺を表しますが、有向グラフでは向きが逆の異なる弧を表します。

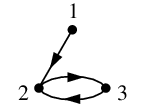
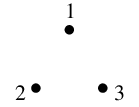
Ex.2　頂点集合と弧集合が $V=\{\,1,2,3\,\}$, $A=\{\,12,23,32\,\}$ である有向グラフを描け。