前へ / 戻る / 次へ $\newcommand{\ol}[1]{\overline{#1}}$ $\newcommand{\card}[1]{\left|\,#1\,\right|}$

サイトの重要度の考え方

　検索サイトは、検索キーワードにヒットした Web ページに何らかのランク付けをして、上位のページから順に提示しています。 Google では PageRank と呼ばれる指標を計算している と言われていますが、 その原則は

• 沢山のサイトからリンクされているサイトは重要である
• 重要なサイトからリンクされていると更に重要である

というものです。

　たとえば $X$ というサイトは、重要度が $x$ で、$n$ 個のサイトに対してリンクを張っているとします。 このとき、$X$ からリンクを張られている $n$ 個のサイトはそれぞれ $\dps{\frac{x}{n}}$ だけの重要度をこのリンクから得ていると考えます。 すなわち という計算をしようという訳です。 ところが リンク元のサイトの重要度も未知数であること が問題で、 こういう式を全てのサイトについて連立させて解かなければいけません。

重要度の計算方法

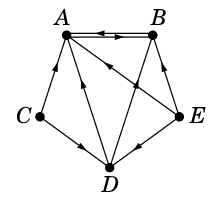
　例えば世の中に5個のサイト $A$, $B$, $C$, $D$, $E$ があって、 それらの間のリンク関係が次の図のようになっていたとしましょう。 $A$, $B$, $C$, $D$, $E$ の重要度を $a$, $b$, $c$, $d$, $e$ とすると、 $a$ の計算式は \begin{align} a &= \frac{b}{B\ のリンク数} + \frac{c}{C\ のリンク数} + \frac{d}{D\ のリンク数} + \frac{e}{E\ のリンク数} \\ &= \frac{b}{1} + \frac{c}{2} + \frac{d}{2} + \frac{e}{3} \end{align} ということになります。$b$, $c$, $d$, $e$ についても計算式を書いて、行列の形にまとめると $$ \left( \begin{array}{c} a \\ b \\ c \\ d \\ e \end{array} \right) = \left( \begin{array}{ccccc} \;0\; & \;\;1\;\; & 1/2 & 1/2 & 1/3 \\ 1 & 0 & 0 & 1/2 & 1/3 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1/2 & 0 & 1/3 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right) \left( \begin{array}{c} a \\ b \\ c \\ d \\ e \end{array} \right) $$ となります。よく見ると ${}^t(a,b,c,d,e)$ はこの行列の固有値 1 に対する固有ベクトルになっていますね。 従って とは言ってもその行列は巨大なものですので、相当工夫をして固有ベクトルを計算しているのでしょう。

前へ / 戻る / 次へ