組合せとグラフの理論(塩田)第12回 (3) 最大フローアルゴリズム
アイデア
最大フローを求めるアルゴリズムのアイデアは割とシンプルです。
アイデア 問 1 のネットワーク
$\varphi$ : 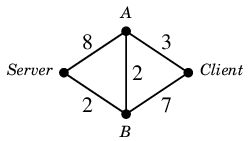
では、例えば次のフロー $\varphi$ は簡単に思いつきます。
$\varphi$ : 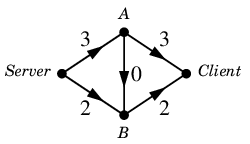
まだ回線容量には余裕があって、あとどの位容量に余裕があるかを書き出すと
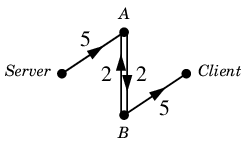
となります。この「残りのネットワーク」の中ではさらに次の
道の形のフロー $\varepsilon$ が見つかります。
$\varepsilon$ : 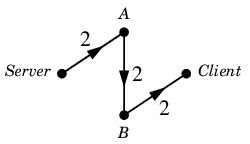
各弧で容量を足して
新 $\varphi=\varphi + \varepsilon$
とおくと、これは最大フローになっています。
新 $\varphi$ : 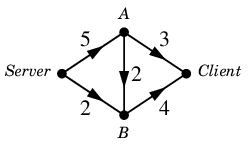 ※
※ このように
- 各回線の容量の残りはいくつか
- その「残り」の中でどれだけフローの値を増やせるか
を考えます。
記号での表現
Def.9(「残り」の表し方) ネットワーク $N=(D,\Psi)$ のフロー $\varphi$ があたえられたとき、
その残りを表すネットワーク $N'=(D,\Psi')$ を次で定める。
$\left\{
\begin{array}{l}
\Psi'(a)=\Psi(a)-\varphi(a) \\
\Psi'(a^{-1})=\Psi(a^{-1})+\varphi(a) \\
\end{array}
\right.$
$\forall a \in A$
ただし $a^{-1}$ は $a$ と逆向きの弧を表す。
$a^{-1}$ を考える理由は後述します。
Def.10( $\varepsilon$ の見つけ方) 上記の $N'$ の中で、
正の容量を持つ弧からなる $v$-$w$ 道 $P$ が存在するとき、
$P$ 上の弧の「残りの容量」の最小値を
$\dps{m=\min_{a \in P} \Psi'(a)}$
とおいて、$P$ 上の弧に重み $m$ を与えたフローを $\varepsilon$ とする:
$\varepsilon(a)=
\left\{
\begin{array}{ll}
m & a \mbox{ が } P \mbox{ 上の弧のとき } \\
0 & \mbox{ otherwise} \\
\end{array}
\right.$
$\varepsilon$ を「増加道(フロー増加道)」と呼ぶ。
上の
アイデア の例では
$P$ : 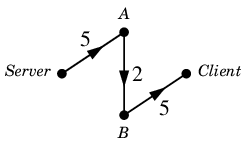
が $N'$ の中の $v$-$w$ 道であり、
真ん中が一番細いので それに太さを揃えたのが $\varepsilon$ です。
$\varepsilon$ が「増加道」であれば
新 $\varphi=\varphi + \varepsilon$
は $\varphi$ よりフローの値が大きいフローとなります。
( $+\varepsilon$ しても「流入量 = 流出量」が成り立つように「太さを揃え」ました。 )
そして次の定理が肝
( きも ) です。
Th.11 ネットワーク $N=(D,\Psi)$ のフロー $\varphi$ が最大フローであることと、
$N'$ が増加道を持たないことが同値である。
証明は次回やります。この定理により
最大フローアルゴリズム
Algorithm 12(最大フローアルゴリズム)
- 入力:ネットワーク $N$
- 出力:$N$ の最大フロー $\varphi$
$\varphi=$ 適当なフロー
while True:
$N'=$ (
Def.9 のネットワーク )
if $N'$ に $v$-$w$ 道 $P$ が存在:
$\varepsilon=$ (
Def.10 の増加道 )
新 $\varphi=\varphi + \varepsilon$
else:
$\varphi$ を出力して終了
- $v$-$w$ 道 $P$ を見つけるには、例えば $N'$ で $v$ を根とする(弧の向きに沿った)幅優先探索を実行します。
- プログラムを組むときは、$\varphi$ の初期値は
$\varphi=$ ゼロフロー $=$ 何も流れていない状態
としますが、人間は賢いのである程度のフローを見つけてから始めます。





