組合せとグラフの理論（塩田）2022年度

組合せとグラフの理論（塩田）第6回 (4)　深さ優先探索

前へ / 戻る / 次へ

深さ優先探索のアルゴリズム

　次は深さを優先して探索します。

Algorithm 15（深さ優先探索、DFS = Depth-First-Search ）

入力：連結なグラフ $G$ と、その頂点 $v$
出力：$v$ を根とする $G$ の深さ優先探索木 $T$

$T$ の初期値は $v$ １点からなる木とし、最初の探索点を $x = v$ とする。
$x$ の未探索隣接点があれば、そのうち番号の一番小さいものを $y$ とする。そうでなければ 4° へ。
$T$ に辺 $xy$ を付加し、$y$ を次の探索点「新 $x$」として 2°へ。
$x=v$ であれば終了。そうでなければ「$x$ の親」を次の探索点「新 $x$」として、2°へ。

ただし「$x$ の親」とは $x$ が探索されたときの探索点のことで、ステップ 4° の操作をバックトラックと呼びます。

Rem.16（ここ大事！）　深さ優先探索の要点は

$T$ には辺は 1 本ずつしか付加しない。
探索点に未探索隣接点がある限り、深く深く 進んでゆく。
探索点に未探索隣接点が無い時は、$T$ の辺をたどって「親」へ戻る。

例題

Ex.17　再び次の二分木で $v=0$ を根として深さ優先探索を実行します。

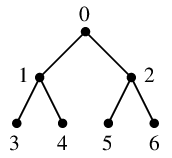
最初の 探索点（青い頂点） は根の $\require{color}\textcolor{blue}{0}$ です。

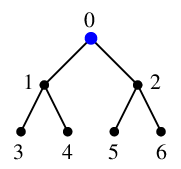
探索点 $\textcolor{blue}{0}$ の未探索隣接点 $1$, $2$ のうち番号の小さい方 $1$ へ進み、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{01}$ を付加、 $\textcolor{blue}{1}$ を新しい探索点とします。

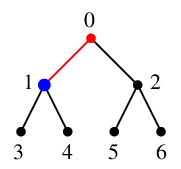
探索点 $\textcolor{blue}{1}$ の未探索隣接点 $3$, $4$ のうち番号の小さい方 $3$ へ進み、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{13}$ を付加、 $\textcolor{blue}{3}$ を新しい探索点とします。

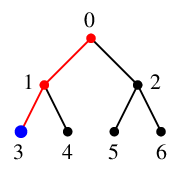
探索点 $\textcolor{blue}{3}$ には未探索隣接点はありませんので、 $3$ の親 $\textcolor{blue}{1}$ へバックトラックします。

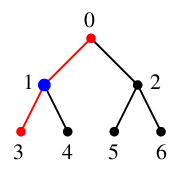
探索点 $\textcolor{blue}{1}$ の未探索隣接点は $4$ のみですので $4$ へ進み、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{14}$ を付加、 $\textcolor{blue}{4}$ を新しい探索点とします。

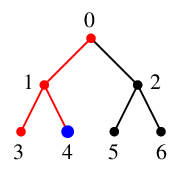
探索点 $\textcolor{blue}{4}$ には未探索隣接点はありませんので、 $4$ の親 $\textcolor{blue}{1}$ へバックトラックします。

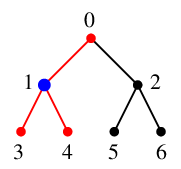
探索点 $\textcolor{blue}{1}$ には未探索隣接点はありませんので、 $1$ の親 $\textcolor{blue}{0}$ へバックトラックします。

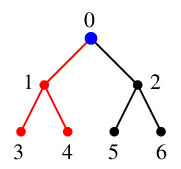
探索点 $\textcolor{blue}{0}$ の未探索隣接点は $2$ のみですので $2$ へ進み、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{02}$ を付加、 $\textcolor{blue}{2}$ を新しい探索点とします。

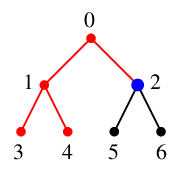
探索点 $\textcolor{blue}{2}$ の未探索隣接点 $5$, $6$ のうち番号の小さい方を $5$ へ進み、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{25}$ を付加、 $\textcolor{blue}{5}$ を新しい探索点とします。

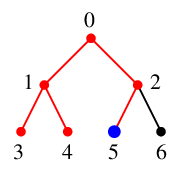
探索点 $\textcolor{blue}{5}$ には未探索隣接点はありませんので、 $5$ の親 $\textcolor{blue}{2}$ へバックトラックします。

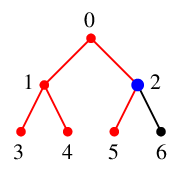
探索点 $\textcolor{blue}{2}$ の未探索隣接点は $6$ のみですので、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{26}$ を付加します。

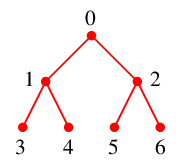
未探索点が無くなりましたので人間がやるときはここでおしまいです。（アルゴリズム的にはこのあと、$0$ までバックトラックして終了です。）

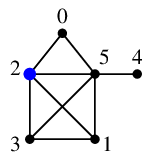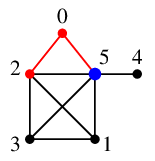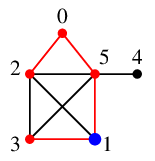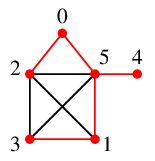
Ex.18　Ex.14 と同じグラフで、今度は $v=2$ を根として深さ優先探索をします。

　根の $\require{color}\textcolor{blue}{2}$ から探索を始めます。

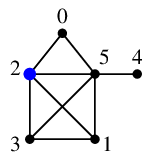
$\require{color}\textcolor{blue}{2}$ の未探索隣接点 $0$, $1$, $3$, $5$ のうち、番号の一番小さい $0$ へ進みます。

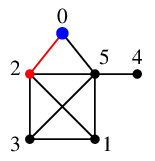
$\require{color}\textcolor{blue}{0}$ の唯一の未探索隣接点 $5$ へ進みます。

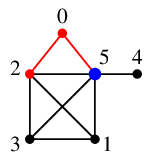
$\require{color}\textcolor{blue}{5}$ の未探索隣接点 $1$, $3$, $4$ のうち、番号の一番小さい $1$ へ進みます。

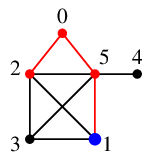
$\require{color}\textcolor{blue}{1}$ の唯一の未探索隣接点 $3$ へ進みます。

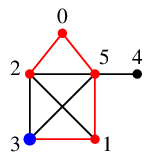
$\require{color}\textcolor{blue}{3}$ には未探索隣接点がありませんので 赤い辺を通って $3$ の親 $1$ へバックトラックします。

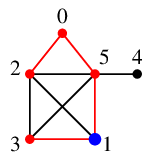
$\require{color}\textcolor{blue}{1}$ にも未探索隣接点がありませんので 赤い辺を通って $1$ の親 $5$ へバックトラックします。

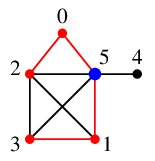
$\require{color}\textcolor{blue}{5}$ の唯一の未探索隣接点 $4$ へ進み、探索終了です。

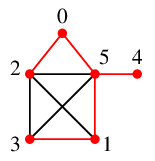
※　こちらも慣れてくればグラフの絵ひとつだけでできるようになります。

深さ優先探索の言い換え

　このアルゴリズムは、スタックを用いて次のように言い換えることができます。

Algorithm 15'（深さ優先探索の言い換え）

入力：連結なグラフ $G$ と、その頂点 $v$
出力：$v$ を根とする $G$ の深さ優先探索木 $T$

空スタック $S=\{\ \}$ を作り、$T$ の初期値は $v$ １点からなる木とする。
探索点を $x=v$ とする。
$x$ の未探索隣接点があれば、そのうち番号の一番小さいものを $y$ とする。そうでなければ 5° へ。
$S$ の先頭に $x$ を追加し、$T$ には辺 $xy$ を付加する。探索点を $x=y$ として 3°へ。
$S$ が空(くう)であれば終了。そうでなければ $S$ の先頭から $x$ を取り出して探索点とし、3°へ。

Ex.17 をスタックを用いて言い換える

Ex.17 をスタックを用いて言い換えます。

1°　最初は、スタック $S$ は空、赤い部分が $\require{color}\textcolor{red}{T}$ です。

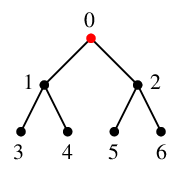$S=\{\ \}$ 2°　探索点（青い頂点）を $\textcolor{blue}{x=0}$ とします。

3°　探索点 $\textcolor{blue}{x=0}$ の未探索隣接点 $1$, $2$ のうち番号の小さい方を $y=1$ とします。

4°　$S$ の先頭に $x=0$ を追加し、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{01}$ を付加、探索点を $\textcolor{blue}{x=1}$ とします。

$S=\{\,0\,\}$ 3°　探索点 $\textcolor{blue}{x=1}$ の未探索隣接点 $3$, $4$ のうち番号の小さい方を $y=3$ とします。

4°　$S$ の先頭に $x=1$ を追加し、 $\textcolor{red}{T}$ には辺 $\textcolor{red}{13}$ を付加、探索点を $\textcolor{blue}{x=3}$ とします。

$S=\{\,1,0\,\}$ 3°　探索点 $\textcolor{blue}{x=3}$ には未探索隣接点はありませんので 5° へ。

5°　$S$ の先頭から $\textcolor{blue}{x=1}$ を取り出して探索点とし、3° へ。

$S=\{\,0\,\}$ 3°　探索点 $\textcolor{blue}{x=1}$ の未探索隣接点は $4$ のみですので $y=4$ とします。

4°　$S$ の先頭に $x=1$ を追加し、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{14}$ を付加、探索点を $\textcolor{blue}{x=4}$ とします。

$S=\{\,1,0\,\}$ 3°　探索点 $\textcolor{blue}{x=4}$ には未探索隣接点はありませんので、 5° へ。

5°　$S$ の先頭から $\textcolor{blue}{x=1}$ を取り出して探索点とし、3° へ。

$S=\{\,0\,\}$ 3°　探索点 $\textcolor{blue}{x=1}$ には未探索隣接点はありませんので、 5° へ。

5°　$S$ の先頭から $\textcolor{blue}{x=0}$ を取り出てし探索点とし、3° へ。

$S=\{\ \}$ 3°　探索点 $\textcolor{blue}{x=0}$ の未探索隣接点は $2$ のみですので $y=2$ とします。

4°　$S$ の先頭に $x=0$ を追加し、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{02}$ を付加、探索点を $\textcolor{blue}{x=2}$ とします。

$S=\{\,0\,\}$ 3°　探索点 $\textcolor{blue}{x=2}$ の未探索隣接点 $5$, $6$ のうち番号の小さい方を $y=5$ とします。

4°　$S$ の先頭に $x=2$ を追加し、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{25}$ を付加、探索点を $\textcolor{blue}{x=5}$ とします。

$S=\{\,2,0\,\}$ 3°　探索点 $\textcolor{blue}{x=5}$ には未探索隣接点はありませんので、5° へ。

5°　$S$ の先頭から $\textcolor{blue}{x=2}$ を取り出して探索点とし、3° へ。

$S=\{\,0\,\}$ 3°　探索点 $\textcolor{blue}{x=2}$ の未探索隣接点は $6$ のみですので、$y=6$ とします。

4°　$S$ の先頭に $x=2$ を追加し、 $\textcolor{red}{T}$ に辺 $\textcolor{red}{26}$ を付加、探索点を $\textcolor{blue}{x=6}$ とします。

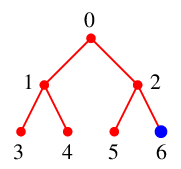$S=\{\,2,0\,\}$ 　未探索点が無くなりましたので人間がやるときはここでおしまいです。（アルゴリズム的にはこのあと、$2$, $0$ を $S$ から取り出して $S$ が空になって終了します。）

前へ / 戻る / 次へ