組合せとグラフの理論（塩田）第6回 (2) 全域木
全域木
これもまず定義から。
Def.7 連結なグラフ $G$ の部分グラフ $T$ が「$G$ の全域木である」とは、
- $T$ は木で、
- $G$ のすべての頂点を含むこと
※ 連結性を保ったまま、ギリギリまで辺を除去した状態 が全域木です。
コンピュータネットワークを表すグラフでは、回線が次々障害を起こして切れてしまって、
まだどのコンピュータ間も通信が可能な状態、と言えばわかるでしょうか。
全域木はテキトーにも描けますが、もっと機械的に求めるルールがあります。
その準備として
キューとスタック
Def.9 要素を一列に並べたデータ構造を「線形リスト」と言う。
線形リストのうち、要素の追加・取り出し方法が特別なもの 2 つを定義する。
- キュー ： 新しい要素はリストの最後尾に追加し、リストの先頭から要素を取り出す
- スタック： 新しい要素はリストの先頭に追加し、リストの先頭から要素を取り出す
それぞれ別の呼び方として、
- キュー = FIFO ( First-In-First-Out )： 先に追加されたものから先に処理される
- スタック = LIFO ( Last-In-First-Out ) ： 最後に追加されたものが先に処理される
Ex.10
- レジに並ぶお客さん（待ち行列）は、先に並んだ人から順番に支払いをするのでキューになります。
- コンビニのペット飲料も、後ろから補給して一番前のものから売れてゆくのでキューになります。
- 本屋さんで山積みになった雑誌は、最後に乗せた一番上の物から売れてゆくのでスタックになります。
- スーパーマーケットの買い物カゴも、最後に重ねた一番上のカゴから取ってゆくのでスタックになります。
※ 「レジに並ぶのがキュー、そうでない方がスタック」と覚えればいいかもしれません。
※
昔ながらの竹の水鉄砲
は、前の穴から吸い込んだ水をキューっと押し出す。ってこれはスタックの方でしたね、失礼しました。
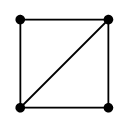のとき、
次の部分グラフはいずれも $G$ の全域木です。
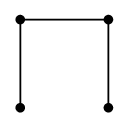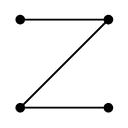とか
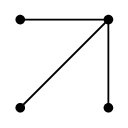とか
とか