組合せとグラフの理論（塩田）第13回 (3) 最大フロー・最小カット定理
最大フロー・最小カット定理
そしていよいよ、驚くべき定理です。 $N'$ を 前回の「残りを表すネットワーク」とし、次の定理と一緒に証明しましょう。 Th.9 の証明 $\Rightarrow$) は前回示しました。逆に、$N'$ が増加道を含まないと仮定して、$\varphi$ が最大フローであることを導きましょう。- $N'$ において入口 $v$ から到達可能な頂点全ての集合を $S$ と置きます。 もちろん $v \in S$ であり、また $N'$ には増加道が無いので $w \not\in S$ ですから $K=(S,\ol{S})$ は $N$ のカットになります。
- $a=xy\in K=(S,\ol{S})$ を任意に取ります。 もし $\Psi'(a) \gt 0$ であれば、$N'$ の中の $v$-$x$ 道と $a=xy$ をつなげば $v$-$y$ 道が作れるので $y \in \ol{S}$ であることに矛盾します。 従って $\Psi'(a) = 0$ でなければなりません。
- $N'$ の作り方から
$\Psi'(a) = \Psi(a) - \varphi(a) + \varphi(a^{-1})$ ですが、フローの条件より $\varphi(a) \leqq \Psi(a)$, $\varphi(a^{-1}) \geqq 0$ ですから、2° により $\varphi(a) = \Psi(a)$ かつ $\varphi(a^{-1}) = 0$ が言えます。 $a^{-1}$ は $(\ol{S}, S)$ の弧ですから、結局- $K=(S,\ol{S})$ の全ての弧 $a$ に対して $\varphi(a)=\Psi(a)$
- $(\ol{S},S)$ の全ての弧 $a$ に対して $\varphi(a)=0$
- 3° と Th.5 より ( $\varphi$ の値 ) $= \Psi(K)$ となり、 Th.7 より $\varphi$ は最大フローです。同時に Th.8 も証明できました。(証明終)
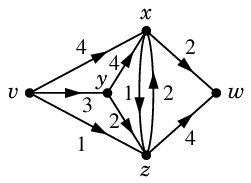
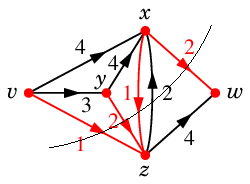
最大フロー・最小カットの例
Ex.11（教科書 p.183）
$N$ : 
の最大フローは
$\varphi$ : 
でした。Th.5 の等号条件をヒントに対応する最小カット $K$ を探すと次の赤い弧たちがそうです。
記号で書くと、$S=\{\,v,x,y,z\,\}$, $\ol{S}=\{\,w\,\}$ として $K=(S,\ol{S})$ になります。
また
も最小カットです。こちらは $S=\{\,v,x,y\,\}$, $\ol{S}=\{\,w,z\,\}$ の場合です。