前へ / 戻る / 次へ $\newcommand{\as}{^{\ast}}$

閉路とカットセットの双対性

　$G$ を連結な平面グラフ、$G\as$ をその双対グラフとし、辺の一対一対応 $e$ $\longleftrightarrow$ $e\as$ によって $G$, $G\as$ の辺の部分集合 $C$, $C\as$ が対応しているとします。 $C$ $\longleftrightarrow$ $C\as$ このとき 証明　 (1) の $\Rightarrow$ )　 $C$ がカットセットならば $G-C$ の頂点 ( $=$ $G\as$ の面 ) は 2 つのグループに分かれますから、 $C\as$ はそのグループ同士の境界線を含みます。 カットセットの極小性から $C\as$ は丁度その境界線に一致し、境界線は閉路ですので $C\as$ は閉路になります。

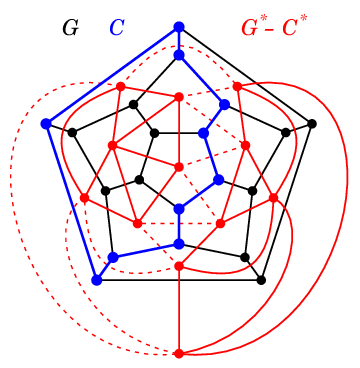
　例えば正十二面体グラフ $G$ とその双対グラフ $G\as$ の場合、

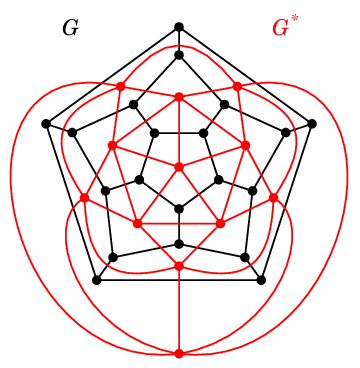
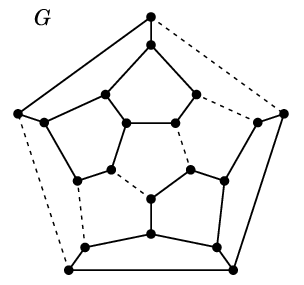
図の点線部分のようにカットセット $C$ を取ると、 対応する $C\as$ は図の(点線の辺をまたぐ)赤い辺たちとなり、閉路になります。

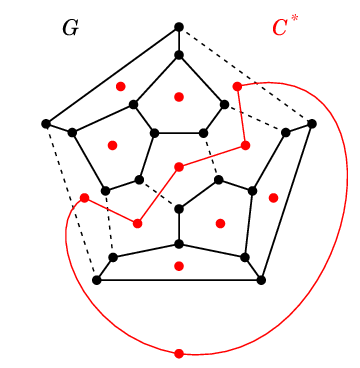
(2) の $\Rightarrow$ )　 $C$ が閉路なら $C$ の内側にも外側にも面（ $=$ $G\as$ の頂点 ) があるので、 $G\as-C\as$ は 2 つの連結成分に分かれます。 $C\as$ の辺を 1 本でも元へ戻すと連結になりますので $C\as$ はカットセットです。

　(1) と同じグラフ $G$ で図の青い部分のように閉路 $C$ を取ると、

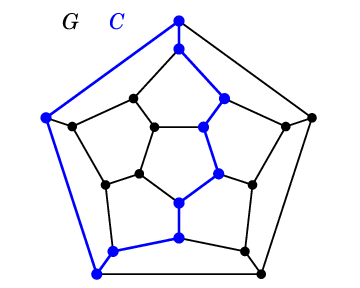
(青い辺をまたぐ)赤い点線の部分が $C\as$ となり、$G\as-C\as$ を 2 つの連結成分に分けるカットセットとなっています。

(1), (2) の $\Leftarrow$ )　は $G$ と $G\as$ を逆にすると言えます。(証明終)

前へ / 戻る / 次へ